rachelmaddie
Full Member
- Joined
- Aug 30, 2019
- Messages
- 851
and side p = 9Okay, it's difficult to tell exactly what you are given with which to begin. I am assuming you are given side \(r=11\) and \(\angle P=37^{\circ}\). Is this correct?
It tells you that the angle is obtuse?Okay, as you did, I would begin with the Law of Sine to determine angle \(R\)
[MATH]\frac{\sin(R)}{11}=\frac{\sin\left(37^{\circ}\right)}{9}[/MATH]
[MATH]\sin(R)=\frac{11\sin\left(37^{\circ}\right)}{9}[/MATH]
[MATH]R=\arcsin\left(\frac{11\sin\left(37^{\circ}\right)}{9}\right)\approx47.4^{\circ}\quad\checkmark[/MATH]
But, we must also consider:
[MATH]R=180^{\circ}-\arcsin\left(\frac{11\sin\left(37^{\circ}\right)}{9}\right)\approx132.6^{\circ}[/MATH]
Do you see why?
132.6 + 47.4 = 180 degreesIt tells you that the angle is obtuse?
It tells you that the angle is obtuse?
I’m a little confused with this concept.Well, in one possible solution, we do find that \(R\) is obtuse, but in the SSA case (where we are given 2 sides and an angle) we find this can be the so-called "ambiguous case," that is we may find two distinct triangle that fit the given data. Recall the identity for sine:
[MATH]\sin(180^{\circ}-x)=\sin(x)[/MATH]
Since 47.4 > 37, we know the supplementary angle to \(47.4^{\circ}\) will also work, because this difference allows for a positive value for the third angle in the second case.
Does this make sense?
I’m a little confused with this concept.
You mean the law of sines?The ambiguous case is confusing at first to most students. Do you understand the identity for sine?
I can not say that I am able to visualize that.It can be derived using the angle difference formula for sine, but the way I visualize it is to picture the unit circle, and a first point at (1,0) and a second point at (-1,0).
Let the first point begin moving at a constant speed around the circle in a counter-clockwise direction, while at the same time the second point begins moving at the same speed but in a clockwise direction.
The \(y\)-coordinate of the first point can represent \(\sin(x)\) while the \(y\)-coordinate of the second point can represent \(\sin(180^{\circ}-x)\).
Can you see that the \(y\)-coordinates of the two points will always be the same?
I can not say that I am able to visualize that.
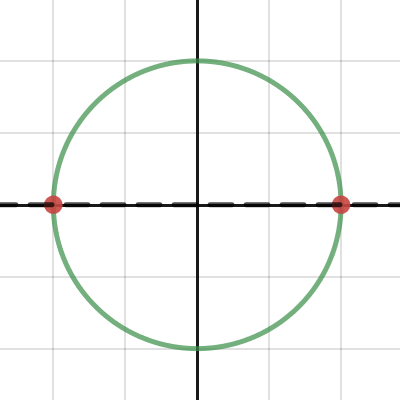
Press the play button?Here's a live graph to help:

Desmos | Graphing Calculator
www.desmos.com
Move the slider on the left at the bottom, and notice the two points are always on the same horizontal dashed line.

ah thank you! Were we done with the question?Yes, or you can manually drag the slider (the circular button under the t value) left and right.
