Geometric or trig subs to find this area? Or do I need to use calculus?

[aecook10]

I’m stumped trying to remember how or if this is possible to answer with the information I have!
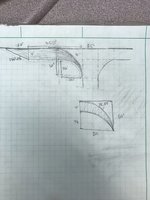
so, the shaded region between the arches in the square is what I’m having trouble finding. The arc length of the top arc is easy cuz it’s just a quarter of the circumference of the circle. (This isn’t homework, it’s actually a picture of a 4 ft shoulder addition on a roadway that will merge into an existing radius). This might be crossing into integration, so apologies if in the wrong feed. I can solve an integration but I’m unsure how to acquire an equation of this line to get an area under this curve. Is there another way to solve this? Thanks for any tips!!!

 

[lev888]

If the bottom curve consists of an arc (right) and a straight line (left) I think you can represent the bottom area as a rectangle (under the straight line) and another quarter(?) circle.

 

[Dr.Peterson]

It all depends on what the bottom curve is.

As lev888 suggested, it could be a 46 by 4 rectangle on the left, and a 46-foot quarter circle.

If it's a quarter ellipse, it's even easier; the area under that curve is just 46/50 of the area of the 50-foot quarter circle.

Whatever it is, you will just subtract the area under the bottom curve from the area of the 50-foot quarter circle (assuming that's what the top curve is).

 

[aecook10]

I went with the 46x4 rectangle, and 46x46 triangle. This works out well since having the extra material doesn’t hurt. ? thank you for the suggestions!!