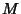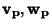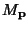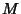My question is regarding the definition of fundamental forms. Let
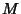 be a Regular Surface with
be a Regular Surface with
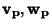 points on the Tangent Space
points on the Tangent Space
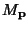 of
of
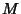 . Then the first fundamental form is the Inner Product of tangent vectors. My question is how do I know which two points to use in the tangent space? I know how to use the other definitions that use surfaces with two parameters defining them, but I was wondering how to get the fundamental forms for higher dimensional or surfaces defined by more than one parameter? Would more parameters/higher dimensions require more tangent points? Can I just pick any two tangent points in the tangent space of the manifold? Thanks. -JS
. Then the first fundamental form is the Inner Product of tangent vectors. My question is how do I know which two points to use in the tangent space? I know how to use the other definitions that use surfaces with two parameters defining them, but I was wondering how to get the fundamental forms for higher dimensional or surfaces defined by more than one parameter? Would more parameters/higher dimensions require more tangent points? Can I just pick any two tangent points in the tangent space of the manifold? Thanks. -JS