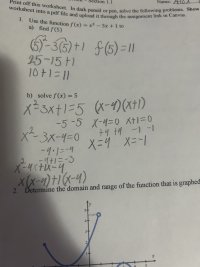Functions

[kenshin3]

So I’m in a college algebra class and have never been good at nor understood math too well and would really like to understand as much as I can. I’m stuck on a problem that’s f(x)=5. F(x)=x^2-3x+1 and I’ve came to two different solutions using the quadratic formula and by factoring and I’ve also found many different solutions trying to solve it on the internet which has only confused me more I can’t even find what exactly it means when the function is written like that [f(x)=5] I know how to solve simpler functions like f(5) but not this one and my class also moves really fast and didn’t show any examples like this one but if anyone could tell me what it means when the function is written that way or show me the steps to solve it I would really appreciate it

 

[Otis]

f(x)=5. F(x)=x^2-3x+1

Hi. f(x) is called function notation, and it's a different way to write y.

y = x^2 – 3x + 1

Now, if I write y = -1, then it doesn't show what value of x generates -1 for y.

Function notation shows it:

f(2) = -1

 

[Otis]

Oops, I hit the post button.

y = f(x) = x^2 – 3x + 1

Example: f(2) = -1

The equation f(2) = -1 tells us that y is -1 when x is 2, and the name of the function is f.

When they ask to solve f(x)=5, it means find the value(s) of x to make y=5.

What solutions did you get from using the quadratic formula? Please show your work; you may post a picture.

 

[Otis]

Also, because you said you couldn't factor the polynomial, let's make sure that you put the equation into standard form before trying to factor or use the quadratic formula. That form has zero on one side:

ax^2 + bx + c = 0

You have

x^2 – 3x + 1 = 5

so the first step is to subtract 5 from each side, yes?

The resulting polynomial does factor nicely. You want two numbers whose product is c and whose sum is b.

 

[The Highlander]

So I’m in a college algebra class and have never been good at nor understood math too well and would really like to understand as much as I can. I’m stuck on a problem that’s f(x)=5. F(x)=x^2-3x+1 and I’ve came to two different solutions using the quadratic formula and by factoring and I’ve also found many different solutions trying to solve it on the internet which has only confused me more I can’t even find what exactly it means when the function is written like that [f(x)=5] I know how to solve simpler functions like f(5) but not this one and my class also moves really fast and didn’t show any examples like this one but if anyone could tell me what it means when the function is written that way or show me the steps to solve it I would really appreciate it

Hi @kenshin3

Welcome to the forum.

As @Otis has explained, if you are given the function \(\displaystyle f(x)=x^2-3x+1\) and told that f(x) = 5 then what that means is that \(\displaystyle x^2-3x+1=5\) and you need to find the value(s) of x that will make that equation true.

You say:-

I’ve came come to two different solutions using the quadratic formula and by factoring...

But the expression \(\displaystyle x^2-3x+1\) doesn't factorize! So I'm not at all sure what you were doing (or thought you were doing, lol)

However, once you have the equation: \(\displaystyle x^2-3x+1=5\) you can re-arrange that to give: \(\displaystyle x^2-3x-4=0\) and that does factorize (quite nicely), thus allowing you to find two values of x that would make it true.

Does that help?

Are you able to factorize it now? You should get (x + ? )(x + ? ) = 0 and that gives you the possible values for x.

Let us know if you still can't figure it out (but show us what you have tried, so we can see what's going wrong)

NB: In the brackets (above) it may or may not be a "+" sign inside them.

Hope that helps.

 

[kenshin3]

Hi @kenshin3

Welcome to the forum.

As @Otis has explained, if you are given the function \(\displaystyle f(x)=x^2-3x+1\) and told that f(x) = 5 then what that means is that \(\displaystyle x^2-3x+1=5\) and you need to find the value(s) of x that will make that equation true.

You say:-

But the expression \(\displaystyle x^2-3x+1\) doesn't factorize! So I'm not at all sure what you were doing (or thought you were doing, lol)

However, once you have the equation: \(\displaystyle x^2-3x+1=5\) you can re-arrange that to give: \(\displaystyle x^2-3x-4=0\) and that does factorize (quite nicely), thus allowing you to find two values of x that would make it true.

Does that help?

Are you able to factorize it now? You should get (x + ? )(x + ? ) = 0 and that gives you the possible values for x.

Let us know if you still can't figure it out (but show us what you have tried, so we can see what's going wrong)

NB: In the brackets (above) it may or may not be a "+" sign inside them.

Hope that helps.

Here’s what I got when I factored the equation and I ended with x=4 x=-1

 

[Steven G]

Here’s what I got when I factored the equation and I ended with x=4 x=-1

All looks good to me.

 

[Otis]

I ended with x=4 x=-1

Yes, those x-values check out.

f(x) = x^2 – 3x + 1

f(4) = 16 – 12 + 1 = 5

f(-1) = 1 + 3 + 1 = 5

I have one comment about your work. After you found the two numbers whose product is -4 and whose sum is -3, it looks like you wrote out two steps from a different factoring method (factor by grouping). Those steps are unnecessary because the two numbers you'd just found are what we use to complete the factorization (x + ?)(x + ?). In other words, you may simply replace symbols ? and ? with -4 and 1:

( x – 4)(x + 1)

[imath]\;[/imath]

 

[kenshin3]

Yes, those x-values check out.

f(x) = x^2 – 3x + 1

f(4) = 16 – 12 + 1 = 5

f(-1) = 1 + 3 + 1 = 5

I have one comment about your work. After you found the two numbers whose product is -4 and whose sum is -3, it looks like you wrote out two steps from a different factoring method (factor by grouping). Those steps are unnecessary because the two numbers you'd just found are what we use to complete the factorization (x + ?)(x + ?). In other words, you may simply replace symbols ? and ? with -4 and 1:

( x – 4)(x + 1)

[imath]\;[/imath]

Alright thank you for all the help and advice