Consider the function \(\displaystyle f(x) = x + \sqrt{x^2+1}\) , x belongs to R .
1) Show that f is strictly increasing over R .
2) Show that the two straight lines of equations y=0 and y=2x are asymptotes to (C).
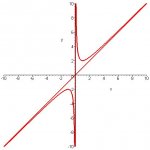
3) Trace (C) .
4)a) Show that f admits an inverse function .
b) Trace the curve of the inverse on same system.
c) Find the equation of the inverse.
5) (D) is the domain limited by (C) , the axix x'x and the two straight lines of equations x=0 and x=1 .
Calculate the volume obtained by rotating (D) about x'x.
My work :
1) The derivative is \(\displaystyle f'(x) = 1 + \frac{x}{\sqrt{x^2+1}}\)
How can I prove it's +ve .
2) Lim[f(x)-0] as x tends to infinity and see if it equals to zero ~~~ Same as Lim[f(x)-2x] as x tends to infinity .
4) f(x) is continuous and defined for all x belongs to R .
f(x) is strictly increasing , monotomic --> f(x) admits an inverse .
b) Symmetry with respect to y=x.
c) \(\displaystyle x-y=\sqrt{x^2+1}\) Square bothe sides ... .. .
5) MmM . . .
Thanks in advance ,
Check my answers , please .
1) Show that f is strictly increasing over R .
2) Show that the two straight lines of equations y=0 and y=2x are asymptotes to (C).
3) Trace (C) .
4)a) Show that f admits an inverse function .
b) Trace the curve of the inverse on same system.
c) Find the equation of the inverse.
5) (D) is the domain limited by (C) , the axix x'x and the two straight lines of equations x=0 and x=1 .
Calculate the volume obtained by rotating (D) about x'x.
My work :
1) The derivative is \(\displaystyle f'(x) = 1 + \frac{x}{\sqrt{x^2+1}}\)
How can I prove it's +ve .
2) Lim[f(x)-0] as x tends to infinity and see if it equals to zero ~~~ Same as Lim[f(x)-2x] as x tends to infinity .
4) f(x) is continuous and defined for all x belongs to R .
f(x) is strictly increasing , monotomic --> f(x) admits an inverse .
b) Symmetry with respect to y=x.
c) \(\displaystyle x-y=\sqrt{x^2+1}\) Square bothe sides ... .. .
5) MmM . . .
Thanks in advance ,
Check my answers , please .