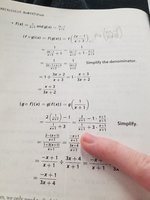Big_Blue824
New member
- Joined
- Nov 23, 2019
- Messages
- 5
Hello!
So I'm doing the thing, and its making sense, but in g(f(x)), theres one bit where I'm not following the book. In the second line of work the book shows, right where my finger is pointing, at the numerator fraction's numerator, the 2 has disappeared from the
2-(x+1)
I've no idea why.
Can someone explain why it's gone?
So I'm doing the thing, and its making sense, but in g(f(x)), theres one bit where I'm not following the book. In the second line of work the book shows, right where my finger is pointing, at the numerator fraction's numerator, the 2 has disappeared from the
2-(x+1)
I've no idea why.
Can someone explain why it's gone?