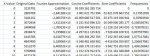
Greetings!I have problems with interpreting Fourier analysis results. What I was trying to do is - determine the phase of business cycles, by analysing GDP dynamics (time series).I have two calculating programmes:1st programme (Fourier transform) resulting data set:see 1st attachment2nd programme (Discrete Fourier transform) resulting data set:see 2nd attachmentBy using this tutorial: http://support.numxl.com/entries/26876407-Discrete-Fourier-Transform-Using-NumXL-WizardBut what should I do with this data - how to perform analysis and interpret it?Thanks!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Fourier transform for GDP data series
- Thread starter Kida
- Start date
Greetings!I have problems with interpreting Fourier analysis results. What I was trying to do is - determine the phase of business cycles, by analysing GDP dynamics (time series).I have two calculating programmes:1st programme (Fourier transform) resulting data set:see 1st attachment2nd programme (Discrete Fourier transform) resulting data set:see 2nd attachmentBy using this tutorial: http://support.numxl.com/entries/26876407-Discrete-Fourier-Transform-Using-NumXL-WizardBut what should I do with this data - how to perform analysis and interpret it?Thanks!
Suppose you have a simple harmonic motion, say a pendulum whose position is given by
p(x) = 5 cos (\(\displaystyle \frac{\pi}{4}\, t\))
That is every eight seconds, it repeats itself [a frequency of 8 Hz]. Suppose you did a Fourier Transform on the data from such a function [sampled the function 128 times over 8 seconds and did an FT on the results], and plotted the FT. You would get a spike at an f (frequency value) of \(\displaystyle \frac{\pi}{4}\) with an amplitude of 5 [depending on just how you scaled you FT]. [Note: you would also get a spike at the negative frequency value but that is an artifact of the FT in this case.]
If you added another cosine term you would get another spike and so forth. The same applies for any function. The frequency component represent a repeat factor of a certain amount and the amplitude of the frequency component represents how strong that component is.