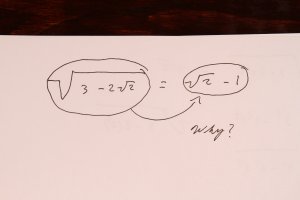Found Serious Hole In My Radical Knowledge

[jddoxtator]

While finishing up the last lessons in Algebra II, I have found a serious hole in my radical knowledge.
When ever there is a binomial under a radical expression that also has a radical, I have no idea how the calculator gets it to the simplest form of one radical to an integer.
I checked all the chapters in the text book about radical equations and expressions, but could find no direct examples of this.
Here is an example of one I can't figure out.

 

[BigBeachBanana]

When ever there is a binomial under a radical expression that also has a radical, I have no idea how the calculator gets it to the simplest form of one radical to an integer.

The equality suggests the expression under the square root can be expressed as a perfect square.

 

[jddoxtator]

The equality suggests the expression under the square root can be expressed as a perfect square.

If it is a perfect square, then is it not equal to the expression under the root sign on the LHS and not the expression on the RHS?
The conjugate give this, but the direct squaring of the LHS gives a trinomial.
I can't see how it can be further rooted, as we already have irrational numbers.

Edit: Ok, I see it now in reverse. Now I just have to work out seeing it forward.

 

[BigBeachBanana]

If it is a perfect square, then is it not equal to the expression under the root sign on the LHS and not the expression on the RHS?

If [imath]\sqrt{3-2\sqrt{2}}=\sqrt{2}-1[/imath], then [imath]3-2\sqrt{2}=(\sqrt{2}-1)^2[/imath]
To confirm, expand [imath](\sqrt{2}-1)^2 =( \sqrt{2})^2-2\sqrt{2}+1=2-2\sqrt{2}+1= 3-2\sqrt{2}[/imath].
These types of expressions are called nested radicals and the process to undo the radical is called denesting. It's not always possible, even if they do, it's often difficult.

These problems are generally (not always) in the form of [imath](a-b\sqrt{c})^2 = a^2-2ab\sqrt{c}+b^2c[/imath].
Here we need [imath]a^2+b^2c = 3[/imath] and [imath]-2ab\sqrt{c}=-2\sqrt{2}[/imath]. From the second equality, [imath]c=2[/imath]. I'll leave it to you as an exercise to solve for [imath]a[/imath] and [imath]b[/imath]. With a lot of experience, you can often spot them pretty quickly, but when starting I used to go through this process.
[imath][/imath][imath][/imath]

 

[jddoxtator]

I think i see it forward now.
What I did was pulled out the root as a factor of the integer and then set the remainder of the integer as the constant term.
I tried to explain best as I can how I was able to see it here in the steps.

 

[BigBeachBanana]

I think i see it forward now.
What I did was pulled out the root as a factor of the integer and then set the remainder of the integer as the constant term.
I tried to explain best as I can how I was able to see it here in the steps.

That's a valid approach.

 

[Steven G]

Did you make sure that sqrt(2) - 1 >0??

Recall that sqrt(x^2) is NOT x, but rather sqrt(x^2) = |x|.

So the answer to you problem would be sqrt(2) - 1 OR 1-sqrt(2). Which one is correct?

 

[jddoxtator]

Did you make sure that sqrt(2) - 1 >0??

Recall that sqrt(x^2) is NOT x, but rather sqrt(x^2) = |x|.

So the answer to you problem would be sqrt(2) - 1 OR 1-sqrt(2). Which one is correct?

Good point, this is from a trigonometric identity so the polarity would be dictated by the parent function.
I was more interested in working the radical out of context so I could apply it to everything and learn the principle.
But yes, you would still have to simplify in polarity terms that make sense for the application.