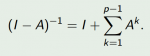Hello
I have been taking a course in Linear Algebra (self-study) and so far I believe I have understood everything I came across (matrix operations and inverses) but this problem just slapped me in the face. It is as follows:
Let A be a square matrix such that (Ap)=0 for some natural p. Prove the following:
. . . . .\(\displaystyle \large{ \displaystyle \left(I\, -\, A\right)^{-1}\, =\, I\, +\, \sum_{k = 1}^{p - 1}\, A^k }\)
I tried to split the identity matrix into A and A^(-1) but that doesn't seem to work... I really have no idea how to come up with that summation...
Thanks in advance
rmp
I have been taking a course in Linear Algebra (self-study) and so far I believe I have understood everything I came across (matrix operations and inverses) but this problem just slapped me in the face. It is as follows:
Let A be a square matrix such that (Ap)=0 for some natural p. Prove the following:
. . . . .\(\displaystyle \large{ \displaystyle \left(I\, -\, A\right)^{-1}\, =\, I\, +\, \sum_{k = 1}^{p - 1}\, A^k }\)
I tried to split the identity matrix into A and A^(-1) but that doesn't seem to work... I really have no idea how to come up with that summation...
Thanks in advance
rmp
Attachments
Last edited by a moderator: