First order critical numbers: f(x)= (x+1) / (x^2+x+1)

R

rachelshelby10

New member
Joined
Apr 12, 2009
Messages
6
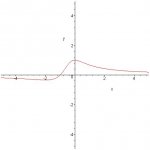
The problem says.. given the function f(x)= (x+1) / (x^2+x+1)... find the first order critical numbers.
**I know that you have to find the first derivative first, and I think I have that part right, but after that you are supposed to set it to zero and find the critical numbers, but I am stuck on what to set to zero and how to get those numbers with dividing polynomials.. this is what I have so far: For the derivative i got: f '(x)= (-x^2 + 3x)/(x^2 + x + 1)^2..... After getting the derivative I'm not sure what to do..... Do I factor first polynomial and set it to zero and solve and do the same with the denominator polynomial ?.....I can solve these problems if it is just one constant polynomial, but I do not like fractions......I'm stuck! :( If anyone can help me it will be greatly appreciated! Thank you in advance!
 
rachelshelby10 said:
… For the derivative i got: f '(x)= (-x^2 + 3x)/(x^2 + x + 1)^2 …
Click to expand...


I get a different result for the first derivative of f(x).

f '(x) = -(x^2 + 2x)/(x^2 + x + 1)^2

Critical numbers are the values of x where the derivative is zero. In other words, solve the following equation for x.

f '(x) = 0

Let me know if you need help solving this equation. Please show whatever work you can accomplish, and try to say something about why you're stuck.

MY EDIT: Fixed typographical error (dropped exponent)
 
BigGlenntheHeavy said:
f(0)=1, f(-2) = -1/3 are the critical numbers …
Click to expand...


Not quite, Glenn.

Unless, by typing the statement above, you were trying to say that 0 and -2 are the critical numbers.

 
Re: First order critical numbers HELP!?!?!

I don't really understand how to get the critical numbers... if you could show me an example it would really help..... and how did you get that derivative?...I don't know where i went wrong... did i even use the right rule?... as for the critical numbers.. what do i set to 0?
 
rachelshelby10 said:
… did i even use the right rule? …
Click to expand...


How would we know? You did not show any of your work calculating the derivative of f.

Did you use the Quotient Rule? (Alternatively, you could factor out the numerator of f, and then use the Product Rule.)

Once you calculate the derivative, find the values of x that make it zero.

Critical numbers are the values of x where the derivative is zero, so it's the derivative that you set equal to zero.

If you would like more help, then please show your work.

 
Re: First order critical numbers HELP!?!?!

mmm4444bot, you are correct. the numbers 0 and -2 are the critical numbers.

(0,1) and (-2,-1/3) are where they are located on the graph of f(x).

I stand corrected, thank you.

Definition of critical number: If f is defined at c, then c is called a critical number of f if f' (c) = 0 or if f' is undefined at c.
 
Re: First order critical numbers HELP!?!?!

I'm sorry I didn't put additional information. I appreciate your help, this is just frustrating me. To get the derivative I used the quotient rule... this is what I got step by step:

f(x)= (x + 1)/(x^2+x+1)

[(x+1) D(x^2 +x +1)-(x^2 +x +1) D(x + 1)]/(x^2 + x +1)^2

[(x + 1)(2x + 1)-(x^2 + x + 1)(1)]/(x^2 + x + 1)^2

[2x^2 + x + 2x + 1- x^2 - x - 1]/(x^2 + x + 1)^2

f '(x)= (x^2 + 2x)/(x^2 + x + 1)^2

This is the derivative I got after I reworked it when you told me you got a different answer and I still can't figure out what I'm doing wrong, because you got something different. I am closer now but I don't understand where the negative came from in front of the numerator and where the square went on the denominator. If you have time to help thanks in advance
 
rachelshelby10 said:
… f(x)= (x + 1)/(x^2+x+1)

[(x+1) D(x^2 +x +1)-(x^2 +x +1) D(x + 1)]/(x^2 + x +1)^2 <<< The derivatives are backwards for the Quotient Rule.

[ D(x + 1) (x^2 + x + 1) - (x + 1) D(x^2 + x + 1) ] / (x^2 + x + 1)^2

… I don't understand … where the square went on the denominator … <<< You correctly squared the denominator.

I made a typographical error in my previous post; I'll fix that.
Click to expand...
 
You must log in or register to reply here.
Top