harrisonhjones
New member
- Joined
- Jul 30, 2008
- Messages
- 1
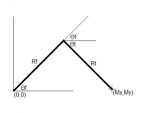
I'm working on an application to simulate a robotic arm with 2 degrees of freedom. I have been controlling the virtual arm so far using track bars which change the different angles of the arm but now I want to be able to click somewhere on the "arena" and have the two "bars" which make up the virtual arm move to "touch" that location. The arm is setup in the usual human arm/elbow configuration. Here's the formula/stuff I have set up so far:
'Constants for each "Equation"
Mx = Mouse X
My = Mouse Y
Rf = Fixed length of the first "bar"
Rt = Fixed length of the second "bar"
?f = Angle of the first "bar"
?t = Angle of the second "bar"
'Rules:
?f <= ?t
?f & ?t <= 90
?f & ?t >= -90
'Formula:
Rf*sin(?f) - My = Rt*Sin(?t + ?f)
I need to solve for ?f and ?t. I realize that there must be multiple solutions but given the three restrictions(See rules) I think there is only one solution. Anybody know how to solve this? I tried using the sin(x + y) = sin(x)*cos(y) + sin(y) * cos(x) but then the work seemed to spiral into insane complexity.
Thanks in advance for any help,
Harrison
P.S. I have attached a picture of the system to help understanding
'Constants for each "Equation"
Mx = Mouse X
My = Mouse Y
Rf = Fixed length of the first "bar"
Rt = Fixed length of the second "bar"
?f = Angle of the first "bar"
?t = Angle of the second "bar"
'Rules:
?f <= ?t
?f & ?t <= 90
?f & ?t >= -90
'Formula:
Rf*sin(?f) - My = Rt*Sin(?t + ?f)
I need to solve for ?f and ?t. I realize that there must be multiple solutions but given the three restrictions(See rules) I think there is only one solution. Anybody know how to solve this? I tried using the sin(x + y) = sin(x)*cos(y) + sin(y) * cos(x) but then the work seemed to spiral into insane complexity.
Thanks in advance for any help,
Harrison
P.S. I have attached a picture of the system to help understanding