Problem:
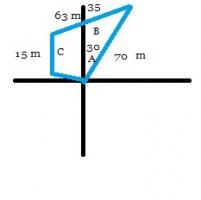
One person is going 70 m and 30 degrees northeast (Vector A)
One person is going 63 m and 35 degrees southwest from the ending point of the first person (Vector B)
One person is going 15 m directly south from the ending point of the 2nd person. (Vector C)
How can we find the vector angles so we can find the x and y components of the displacements?
One person is going 70 m and 30 degrees northeast (Vector A)
One person is going 63 m and 35 degrees southwest from the ending point of the first person (Vector B)
One person is going 15 m directly south from the ending point of the 2nd person. (Vector C)
How can we find the vector angles so we can find the x and y components of the displacements?
Last edited: