Finding the "normal line" of a graph.

[Rumor]

Here's the problem:

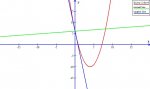
"Given the parabola y = x^2 - Ax +B, where A is the number of letters in your first name and B is the number of letters in your last name, find an equation for the line L that contains the point (0,B) and is perpendicular to the tangent line to the parabola at (0,B). This is called the 'normal line' to the graph."

For me, A = 8 and B = 6. It says that I can find the slope of the tangent line and then use that to compute the slope of the normal line, but I'm not sure how to go about doing that. I know the derivative of the function is y = 2x - A but I don't know where to go from there.

 

[galactus]

By your name, we have \(\displaystyle x^{2}-8x+6\)

The slope at (0,6) is then \(\displaystyle 2(0)-8=-8\), by the derivative.

The normal line will have slope 1/8 because it is the negative reciprocal of -8.

So, using y-mx+b, \(\displaystyle 6=\frac{1}{8}(0)+b\Rightarrow b=6\)

and the normal line equation is \(\displaystyle y=\frac{1}{8}x+6\)

 

[Rumor]

Thank you!

But when I graph the resulting equations, they don't look right together.
It doesn't even look like I come out with a proper tangent line..

 

[galactus]

Here is the graph. Looks good to me.

The tangent line is \(\displaystyle y=-8x+6\) and the normal line equation is \(\displaystyle y=\frac{1}{8}x+6\)

 

[Rumor]

Ah, never mind. I entered the equations wrong. Silly me.

Thank you again. :]