Finding the inverse of: f(x) = 3 + x^2 + tan(pix/2)

[Math_Junkie]

I'm having trouble finding the inverse equation for..

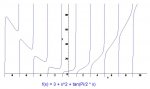
f(x) = 3 + x^2 + tan(pix/2)

Any suggestions on how I can isolate the x? The pix in the tan is causing me some problems.

Thanks!

 

[BigGlenntheHeavy]

Here is its graph, lots of luck.


[attachment=0:14ca5vnj]ggg.jpg[/attachment:14ca5vnj]

 

[mmm4444bot]

Be careful. This function is neither continuous nor one-to-one over its entire domain. (Double-click image, to expand.)

[attachment=0:1qlxch08]Graph.JPG[/attachment:1qlxch08]

 

[Math_Junkie]

I tried graphing as well, but how would I go about getting a formula of the inverse (using algebra)?

 

[Math_Junkie]

Anyone?

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ y \ = \ 3+x^{2}+tan\bigg(\frac{\pi x}{2}\bigg)\)

\(\displaystyle Inverse: \ x \ = \ 3+y^{2}+tan\bigg(\frac{\pi y}{2}\bigg), \ Now, \ solve \ for \ y.\)

 

[Math_Junkie]

That's exactly where I'm stuck. I don't know how to isolate the y from inside the tan bracket.

 

[BigGlenntheHeavy]

Neither do I. In fact, I don't think it can be done. Perhaps some purist has an idea, if we can get one to look at your problem.