You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Finding the Domain
- Thread starter srv96
- Start date
renegade05
Full Member
- Joined
- Sep 10, 2010
- Messages
- 260
Find the domain of each (use interval notation)
√ = square root
1. f(x)= √(x-3)
2. f(x)= x^2+1/x^2-x-6
3. f(x)= √2+x-x^2
You know, I'm somewhat new here, maybe a year and a bit on here now.
I use to post questions like yours. By that I mean, no detail, no work, no nothing.
I always got replies saying "show your work, where are you stuck?" I kinda got annoyed at these responses, just thinking: "OH just tell me the answer".
But now that I have higher level mathematics under my belt and I try to help out on this forum, I see the light!
YOU HAVE TO TELL US WHAT YOU HAVE TRIED AND WHERE EXACTLY YOU ARE STUCK!
Do you know what domain is? Do you know why you cannot have a negative under the square root? Do you know what interval notation is? Do you know how to add? Do you know how to subtract? Do you know how to solve for variables? The questions go on and on.
So where are you stuck ??
Oh sorry, I know that when it under a radical you have to make it less than or equal to 0.
So 1. x-3
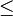 0
0
x
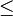 3
3
I don't know where I would go from there to figure out the domain.
2. x^2+1 =0
x^2=1
√x^2-√1
x=1
x^2-x-6=0
(x-3)(x+2)
x=3 x=-2
Again I have no idea where to get the domain from here
3. 2+x-x^2
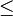 0
0
I don't know how to solve the rest of this because theres 2 x's.
So 1. x-3
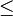
x
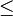
I don't know where I would go from there to figure out the domain.
2. x^2+1 =0
x^2=1
√x^2-√1
x=1
x^2-x-6=0
(x-3)(x+2)
x=3 x=-2
Again I have no idea where to get the domain from here
3. 2+x-x^2
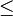
I don't know how to solve the rest of this because theres 2 x's.
\(\displaystyle \text{Ditto what renegade05 posted.}\)Find the domain of each (use interval notation)
2. f(x)= x^2+1/x^2-x-6
--------------------------------------
srv96,
for the second one, did you intend to type:
f(x) = (x^2 + 1)/(x^2 - x - 6) =
\(\displaystyle \dfrac{x^2 + 1}{x^2 - x - 6} \ ?\)
