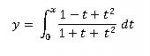finding the derivative of a definite integral

[tehbrosta]

Find the derivative of the following function at x = 1

[attachment=1:1ruxxw1a]3.jpg[/attachment:1ruxxw1a]

Based on the Fundamental Theorem of Calculus, Part I would this be correct?

[attachment=0:1ruxxw1a]3-attempt.jpg[/attachment:1ruxxw1a]



thanks, my teacher to so horrible. I might actually be able to learn something this way.

 

[tkhunny]

Ummm...No.

If

\(\displaystyle f(x) = \int_{0}^{x}g(t)dt\)

then


\(\displaystyle f'(x) = g(x)\)

Please, do not EVER just substitite the value up front. Very bad. This should lead to zero (0) rather consistently. You tell me why this is so. Think about your "2". Just what, exactly is that? Is it a function? Is it a number? is it a vector? What?

Give it another go. Look back up at the first two formulas I wrote.

 

[tehbrosta]

Ummm...No.

If

\(\displaystyle f(x) = \int_{0}^{x}g(t)dt\)

then


\(\displaystyle f'(x) = g(x)\)

Please, do not EVER just substitite the value up front. Very bad. This should lead to zero (0) rather consistently. You tell me why this is so. Think about your "2". Just what, exactly is that? Is it a function? Is it a number? is it a vector? What?

Give it another go. Look back up at the first two formulas I wrote.

Its a function of y

So when I take the derivative at x=1 I get:

\(\displaystyle y'(1) = (1-(1)+1^2)/(1+1+1^2) = 1/3\)

?

 

[tkhunny]

I never understand why questioners decide to argue rather than to learn.

If

\(\displaystyle y\;=\;f(x)\;=\;\int_{0}^{x}g(t)\;dt\)

Then

\(\displaystyle y'\;=\;f'(x)\;=\;g(x)\)

In your problem, we have

\(\displaystyle y\;=\;f(x)\;=\;\int_{0}^{x}\frac{1-t+t^{2}}{1+t+t^{2}}\;dt\)

Then

\(\displaystyle y'\;=\;f'(x)\;=\;\frac{1-x+x^{2}}{1+x+x^{2}}\)

For x = 1 we have f'(1) = (1-1+1)/(1+1+1) = 1/3 as you had it, but there is no way to tell that you understood what you were doing. Notation matters. Clarity matters. Intermediate steps making sense matters.

Normally, this is not acceptable:

1) This is a great problem statement.
2) Then a miracle occurs.
3) This is the correct answer.

The middle part needs some work.