Hey I was wondering if anybody could help me out here.
I'm kind of stuck on this question:
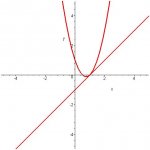
Find the coordinates of the point on the curve y = 2x[sup:3sggzway]2[/sup:3sggzway] - 3x + 1 where the tangent has a gradient 1.
I know how to do these equations the other way around, when having to find the tangent when given the coordinates and the curve, but not this way.
Help??
I'm kind of stuck on this question:
Find the coordinates of the point on the curve y = 2x[sup:3sggzway]2[/sup:3sggzway] - 3x + 1 where the tangent has a gradient 1.
I know how to do these equations the other way around, when having to find the tangent when given the coordinates and the curve, but not this way.
Help??