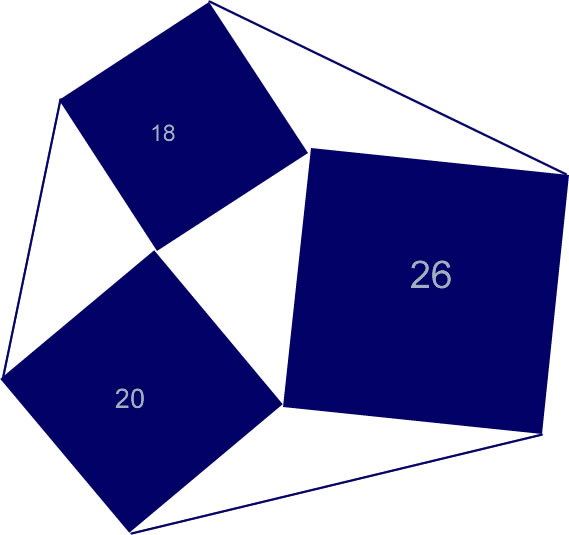
Does anyone have any ideas on how to find the area of the entire region given in this image? The areas of each square are labeled. I am trying to find the area of the the blue squares and white triangles. I think I have found the area of the middle triangle \(\displaystyle (\frac{\sqrt{324}}{2})\). How do I find the outer triangle areas?