The answer turns out to be very simple: the height of the triangle is [MATH]20\cdot\frac{\sqrt{3}}{2} = 17.32[/MATH].
I determined this by first drawing the figure with circles,
View attachment 14019
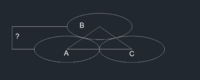
where the equilateral triangle makes it clear that height CD is [MATH]\sqrt{3}[/MATH] times the radius BD; and then using the fact that if we compress the entire figure vertically, we get ellipses in the same relationship, with the vertical ratios unchanged:
View attachment 14020
So the height of the triangle is still [MATH]\sqrt{3}[/MATH] times the vertical semiaxis,10. This is independent of the base of the triangle! So the one fact you omitted in the original question is the one fact needed to answer the question.