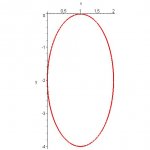
Ok, so given the graph:
4x2 + y2 - 8x + 4y + 4 = 0
Find the coordinates of the points of horizontal and vertical tangents
So for the horizontal tangents I did:
8x + 2y(dy/dx) - 8 + 4(dy/dx) = 0
(dy/dx)(2y+4) = -8x - 8
dy/dx = (-8x-8)/(2y+4)
So to find the x-coordinates:
(-8x-8)/(2y+4) = 0
-8x-8 = 0
x = -1
For the vertical tangents:
8x(dx/dy) + 2y - 8(dx/dy) + 4 = 0
(dx/dy)(-8x - 8) = 2y+4
dx/dy = (2y+4)/(-8x-8)
To find the y-coordinates:
2y+4 = 0
y = -2
My question is...how can I find the y-coordinates of the points of tangency for the horizontal tangents, and how can I find the x-coordinates of the points of tangency for the vertical tangents?
4x2 + y2 - 8x + 4y + 4 = 0
Find the coordinates of the points of horizontal and vertical tangents
So for the horizontal tangents I did:
8x + 2y(dy/dx) - 8 + 4(dy/dx) = 0
(dy/dx)(2y+4) = -8x - 8
dy/dx = (-8x-8)/(2y+4)
So to find the x-coordinates:
(-8x-8)/(2y+4) = 0
-8x-8 = 0
x = -1
For the vertical tangents:
8x(dx/dy) + 2y - 8(dx/dy) + 4 = 0
(dx/dy)(-8x - 8) = 2y+4
dx/dy = (2y+4)/(-8x-8)
To find the y-coordinates:
2y+4 = 0
y = -2
My question is...how can I find the y-coordinates of the points of tangency for the horizontal tangents, and how can I find the x-coordinates of the points of tangency for the vertical tangents?