Gouskin
New member
- Joined
- May 30, 2013
- Messages
- 30
Firstly, I'm in prealculus, so I don't really know any of the notation
Is there a theorem to find the equation of a summation that would allow me to sum the terms from, say, 1 to 2.6?
For example:
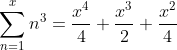
And if x is all real numbers, the equation in summation notation won't return an answer for any non integers, while the equation in standard notation will.
So, if x = 2, it returns 9, and if x = 2.6, it returns 21.9024
The formula, though I don't know if this works for everything, I can get down so far is:
=\int%20f\left%20(%20x%20\right%20)+\frac{f\left%20(%20x%20\right%20)}{2}+\frac{\frac{\mathrm{d}%20f\left%20(%20x%20\right%20)}{\mathrm{d}%20x}}{12}+can't%20figureitoutlol)
where
=x^2) or
or
=x^3) or some variation or whatever up until x^5, in which case it converges quickly but is not exact.
or some variation or whatever up until x^5, in which case it converges quickly but is not exact.
(Doesn't work when the derivative does not contain x or something. I don't know how to describe it because I'm not in calculus!)
Any help on completing the pattern?
Anyone already know the pattern?
Is there a theorem to find the equation of a summation that would allow me to sum the terms from, say, 1 to 2.6?
For example:
And if x is all real numbers, the equation in summation notation won't return an answer for any non integers, while the equation in standard notation will.
So, if x = 2, it returns 9, and if x = 2.6, it returns 21.9024
The formula, though I don't know if this works for everything, I can get down so far is:
where
(Doesn't work when the derivative does not contain x or something. I don't know how to describe it because I'm not in calculus!)
Any help on completing the pattern?
Anyone already know the pattern?
