Finding critical numbers of this function?

[thattoneegurll]

I need to know how to find the critical numbers of this function:

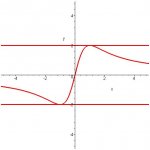
f(x) = 4x / x^2 + 1

I think I already found the derivative, which is:

f'(x) = 4x^2 + 4 / (x^2 + 1)^2

I just have a problem setting it equal to zero to find the critical numbers :/ help plzz?

 

[wjm11]

f'(x) = 4x^2 + 4 / (x^2 + 1)^2

I just have a problem setting it equal to zero to find the critical numbers :/ help plzz?

Close, but you are missing a "-" sign:

f'(x) = (-4x^2 + 4 )/ (x^2 + 1)^2

When setting a rational expression equal to zero, it is only necessary to set the numerator equal to zero and solve that. If the numerator equals zero, the whole expression will equal zero (as long as the denominator does not equal zero, too):

0 = (-4x^2 + 4 )

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ \frac{4x}{x^{2}+1}, \ f \ ' \ (x) \ = \ \frac{4-4x^{2}}{(x^{2}+1)^{2}}\)

\(\displaystyle 4-4x^{2} \ = \ 0 \ \implies \ x \ = \ \pm1, \ f(\pm1) \ = \ \pm2\)

\(\displaystyle Hence, \ the \ critical \ points \ are \ (1,2) \ and \ (-1,-2), see \ graph \ for \ further \ elucidation.\)

[attachment=0:2y2s9gxm]bad.jpg[/attachment:2y2s9gxm]