allhalf425
New member
- Joined
- Oct 19, 2009
- Messages
- 6
How would I find and classify the critical points of a function as follows...
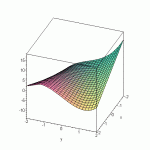
Find and classify the critical points of
z = f(x, y) = x[sup:3alyxftz]2[/sup:3alyxftz] - 2xy + y[sup:3alyxftz]3[/sup:3alyxftz] - y
Find and classify the critical points of
z = f(x, y) = x[sup:3alyxftz]2[/sup:3alyxftz] - 2xy + y[sup:3alyxftz]3[/sup:3alyxftz] - y