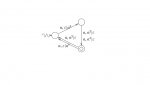
Ok, so given the following automata:

I need to find the language that accepts it (no need for formal prove, a short intuitive explanation is good enough).
I think the answer here is {\(\displaystyle {a^{11+6k},k>=0}\)}.
I can explain why the shortest word that can be received here is \(\displaystyle a^{11}\), and I can explain that this language contains the language {\(\displaystyle {a^{11+6k},k>=0}\)}, but I don't know how to explain that this is exactly the language
{\(\displaystyle {a^{11+6k},k>=0}\)}.
How can you explain that it doesn't conatin more words, for example?
I need to find the language that accepts it (no need for formal prove, a short intuitive explanation is good enough).
I think the answer here is {\(\displaystyle {a^{11+6k},k>=0}\)}.
I can explain why the shortest word that can be received here is \(\displaystyle a^{11}\), and I can explain that this language contains the language {\(\displaystyle {a^{11+6k},k>=0}\)}, but I don't know how to explain that this is exactly the language
{\(\displaystyle {a^{11+6k},k>=0}\)}.
How can you explain that it doesn't conatin more words, for example?