\(\displaystyle g(x) \ = \ ax^{3}+bx^{2}+cx+d\)
\(\displaystyle g(7) \ = \ 1 \ = \ 343a+49b+7c+d\)
\(\displaystyle g(-8) \ = \ 5 \ = \ -512a+64b-8c+d\)
\(\displaystyle g'(x) \ = \ 3ax^{2}+2bx+c\)
\(\displaystyle g'(-8) \ = \ 0 \ = \ 192a-16b+c\)
\(\displaystyle g'(7) \ = \ 0 \ = \ 147a+14b+c\)
\(\displaystyle Using \ reduced \ row \ echelon \ form \ on \ my \ trusty \ TI-89, \ I \ get:\)
\(\displaystyle a \ = \ \frac{8}{3375}, \ b \ = \ \frac{4}{1125}, \ c \ = \ \frac{-448}{1125}, \ and \ d \ = \ \frac{9451}{3375}.\)
\(\displaystyle Hence, \ g(x) \ = \ \frac{8x^{3}}{3375}+\frac{4x^{2}}{1125}-\frac{448x}{1125}+\frac{9451}{3375}\)
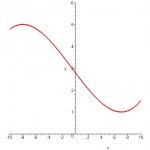
\(\displaystyle See \ graph\)
[attachment=1:kptkc36x]jkl.jpg[/attachment:kptkc36x]
\(\displaystyle Note: \ Further \ elaboration.\)
\(\displaystyle By \ Descartes' \ rule \ of \ signs, \ two \ possibilities \ exist, \ to \ wit:\)
\(\displaystyle - \ + \ I\)
\(\displaystyle \ 1 \ \ 2 \ \ 0\)
\(\displaystyle \ 1 \ \ 0 \ \ 2\)
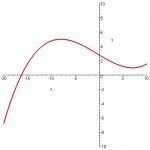
\(\displaystyle And \ since \ the \ max, \ min, \ are \ both \ above \ the \ x-axis, \ the \ only \ possibility \ is \ one \ real \ zero\)
\(\displaystyle \ and \ two \ imaginary \ zeros (second \ one).\)
\(\displaystyle See \ graph \ below, \ zero \ of \ g(x) \ \dot= \ -16.27853, \ note \ also, \ a \ point \ of \ inflection \ around \ x \ = \ 0.\)
[attachment=0:kptkc36x]mno.jpg[/attachment:kptkc36x]