Hi, I have a polar curve, r = theta.
One can find the arc length through integration, eventually coming up with:
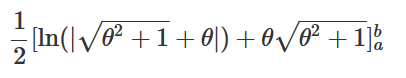
What I would like to do however, is find the upper bound "b" given lower bound "a" and an arc length.
So for example, if I want an arc length of 5, and my lower bound is pi/2, I'd like to know what the upper bound should be:
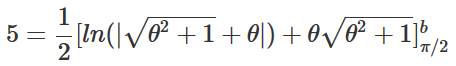
But of course, I'd like to make the arc length anything I desire, along with the lower bound.
After rewriting it.. I believe this can be solved by finding the inverse for the following:
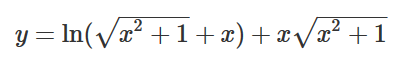
"y" is everything that can be punched into a calculator, so its a "known" variable.
What I tried
I tried to get rid of the natural log:
e^y = (sqrt(x^2+1) +x) * e^(xsqrt(x^2+1)) but now I can't get rid of the e^(..) term..
I tried wolfram to solve it for me.. I tried mathway.. I tried symbolab.. none can solve it.
I'm having a little bit of trouble with this though and I'm not the best with logs.. any general pointers?
Thank you!
One can find the arc length through integration, eventually coming up with:
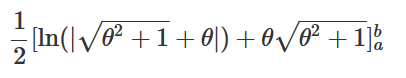
What I would like to do however, is find the upper bound "b" given lower bound "a" and an arc length.
So for example, if I want an arc length of 5, and my lower bound is pi/2, I'd like to know what the upper bound should be:
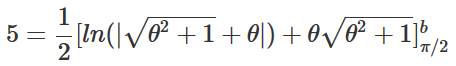
But of course, I'd like to make the arc length anything I desire, along with the lower bound.
After rewriting it.. I believe this can be solved by finding the inverse for the following:
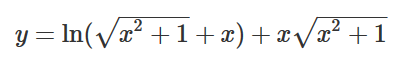
"y" is everything that can be punched into a calculator, so its a "known" variable.
What I tried
I tried to get rid of the natural log:
e^y = (sqrt(x^2+1) +x) * e^(xsqrt(x^2+1)) but now I can't get rid of the e^(..) term..
I tried wolfram to solve it for me.. I tried mathway.. I tried symbolab.. none can solve it.
I'm having a little bit of trouble with this though and I'm not the best with logs.. any general pointers?
Thank you!
Last edited:
