Find the hydrostatic force (having trouble w/ variable-width

[MarkSA]

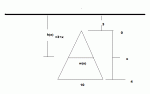
Hello,

We're doing problems where I have to find the hydrostatic force by doing F = PA and putting it into integral form. Most of the problems are taking the shape of: A vertical plate of random shape is submerged in a pool of water. Find the hydrostatic force on one side of the plate.

I'm having a lot of trouble with these. I understand the concepts and the equations, but i'm having a really hard time setting the problem up. In particular, finding the width portion of the Area of a tiny strip of the shape. I'm having the most trouble with triangles/trapezoids where the width changes...

Anyone know of a website that might have a bunch of examples of these I could practice on? Or any tips/tricks on how to handle them?

 

[galactus]

Re: Find the hydrostatic force

Whenever you're confronted with a shape like a triangle, it is a good idea to use similar triangles. Here's an example:

Suppose we have a plate that is an isosceles triangle submerged in water 3 feet below the surface. We know water has density 62.4 lb/ft^3.

The triangle has base width 10 feet and height 4 feet. Find the pressure on the plate.

If we suppose that some point lies h(x) below the surface and the cross section at this point x has width w(x). We can approximate the section of the plate along the kth subinterval by a rectangle of length w(x) and width \(\displaystyle {\Delta}x\).

Then, the force is \(\displaystyle {\rho}h(x)w(x){\Delta}x\)

That is the density times the depth that point is below the surface times the length times the width.

I hope I was able to make that clear. What we are doing is integrating to add up all the areas of the infinite rectangles we have below the surface in order to arrive at the total pressure.

Now, back to the triangle.

By similar triangles, the width of the plate at a depth of h(x)=3+x feet satisfies \(\displaystyle \frac{w(x)}{10}=\frac{x}{4}\)

\(\displaystyle w(x)=\frac{5}{2}x\)

Therefore, the force on the plate is \(\displaystyle F=62.4\int_{0}^{4}(3+x)(\frac{5}{2}x)dx=7072 \;\ lbs\)

The triangle is 4 feet high so we have to integrate from 0 to 4. But it is 3 feet below the surface at the top and then each point down from that to the bottom of the triangle is x. So, we have to use 3+x.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

 

[MarkSA]

Re: Find the hydrostatic force

I think I understand these better now, thanks for the explanation. It helped to think of the width as w(x)

 

[galactus]

Re: Find the hydrostatic force

How about the trapezoidal case?. Are you OK with how to do those?.

 

[MarkSA]

Re: Find the hydrostatic force

Yes I believe so. There was only one in the book to practice on, but I got it correct. It was an isosceles trapezoid which is easier, but I figure that's probably the most difficult one we will be doing in the section.