Find the distance between the centroid of a triangle and a random line $l$

[kaloyan]

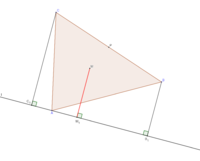
We are given [MATH]\triangle ABC[/MATH] with centroid [MATH]M[/MATH] and a line [MATH]l[/MATH] such that [MATH]A \in l[/MATH] and [MATH]l[/MATH] does not intersect the segment [MATH]BC[/MATH]. Find [MATH]d(M; l)=MM_1[/MATH] if [MATH]CC_1=24[/MATH] and [MATH]BB_1=10[/MATH].
[MATH][/MATH][MATH]B_1BCC_1[/MATH] is a right trapezoid. If [MATH]PP_1 \perp l, P \in l[/MATH], then [MATH]PP_1[/MATH] is the midsegment. This is what I have noticed so far. Would appreciate your help!

 

[Dr.Peterson]

I can think of several ways to approach this: vectors, coordinates, similar triangles, ... .

What methods have you been using that you might be expected to try here? What definition and theorems about the centroid do you have to work with?

Starting with what you have said, I wonder if you have considered the segment AP, and how M is related to it. That can take you directly to the answer.