Find the area bounded by the curve

[MarkSA]

Hello,

My problem is:
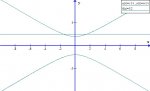
1) Find the area bounded by the curve x = t - 1/t, y = 1 + 1/t, and y = 2.5

I'm not sure how to begin on this, aside from the fact that an integral will come into play. Would I convert it to cartesian form and then take the integral of that? But i'm not sure where the y = 2.5 comes into play. Also i'm not sure how to find the limits. Could you explain the procedure for this type of problem?

 

[galactus]

That's one way to do it.

Looking at the graph, we have a small region bounded by y=5/2 and the upper hlaf of the hyperbola.

Solve \(\displaystyle y=t+\frac{1}{t}\) for t and sub into x.

Solving y for t we get: \(\displaystyle t=\frac{\sqrt{y^{2}-4}}{2}\)

Sub into x and we get \(\displaystyle x=\frac{\sqrt{y^{2}-4}+y}{2}-\frac{2}{\sqrt{y^{2}-4}+y}\)

Now, if you feel brave, you can integrate: \(\displaystyle \int_{2}^{\frac{5}{2}}\left[\frac{\sqrt{y^{2}-4}+y}{2}-\frac{2}{\sqrt{y^{2}-4}+y}\right]dy\)

I would use technology for this. It is very messy.

There is a way t integrate parametrically. \(\displaystyle \int_{t_{1}}^{t_{2}}ydx\). See here: http://www.mathwords.com/a/area_parametric.htm