G
Guest
Guest
Hi everyone, i have a midterm exam coming up and i'm looking at problems in the section of the book to help myself prepare. Can anyone answer this question for me? I have attempted to answer this problem but without the answer i don't know if i'm right.
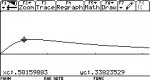
Find the angle theta between vectors r(t) and r'(t) as a function of t. Sketch the graph of theta(t) and find any extrema of theta(t). Find any values of t which the vectors r(t) and r'(t) are orthogonal.
and they give vector r(t) = t^2 ii + t ij
And there are no typos, that's really what the question asks.
I tried using the techniques given in the book but i have NO idea where to go with this problem. I honestly don't even know where to begin, what's the ii and ij all about? I've never seen that before buy my teacher says it's important... how is this calculus I in high school?
Can someone do this one out for me? It's not a homework, i just need to see it done out step by step so i can follow it, along with the answer.
PLEASE help, i'm desperate. Thanks!
Find the angle theta between vectors r(t) and r'(t) as a function of t. Sketch the graph of theta(t) and find any extrema of theta(t). Find any values of t which the vectors r(t) and r'(t) are orthogonal.
and they give vector r(t) = t^2 ii + t ij
And there are no typos, that's really what the question asks.
I tried using the techniques given in the book but i have NO idea where to go with this problem. I honestly don't even know where to begin, what's the ii and ij all about? I've never seen that before buy my teacher says it's important... how is this calculus I in high school?
Can someone do this one out for me? It's not a homework, i just need to see it done out step by step so i can follow it, along with the answer.
PLEASE help, i'm desperate. Thanks!