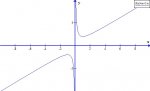
Find the absolute max/min value for f(x) = x + x^(-1), x > 0

[K_Swiss]

Find the absolute maximum and minimum values for:

\(\displaystyle f(x) = x + x^{-1}, x > 0\)

My work:

\(\displaystyle f'(x) = 1 - \frac {1}{x}\)

\(\displaystyle 0 = \frac {x-1}{x}\)

\(\displaystyle x - 1 = 0\)
\(\displaystyle x = 1\)

\(\displaystyle f(1) = 1 + 1^{-1}\)
\(\displaystyle f(1) = 2\)

Critical Point - \(\displaystyle (1, 2)\)

Since \(\displaystyle x > 0\), can pick any x value greater than 0...

\(\displaystyle x = 3\)
\(\displaystyle f(3) = 3 + 3^{-1}\)
\(\displaystyle f(3) = \frac {10}{3}\)

Point\(\displaystyle (3, \frac {10}{3})\)

Therefore, the absolute maximum is at \(\displaystyle x > 0\) and the absolute minimum is at \(\displaystyle (1,2)\)


Am I right, if not, please correct my work.

 

[galactus]

There is a slight mistake.

Your first derivative is \(\displaystyle f'(x)=1-\frac{1}{x^{2}}\)

This gives two solutions. A max at x=-1 and a min at x=1

Here's the graph:

 

[K_Swiss]

Would the critical points be (-1, -2) and (1, 2)?

I don't understand why x = -1 is the max? (1, 2) looks like the local max because of the greater y value? I know the graph proves otherwise, but I need to know how to prove it algebraically

 

[galactus]

Try the second derivative test.

If f''(x)>0 at some point, then f has a relative minimum.

If f''(x)<0 at some point, then f has a relative maximum.

\(\displaystyle f''(x)=\frac{2}{x^{3}}\)

\(\displaystyle f''(1)=2\), therefore it has a relative minimum at x=1

\(\displaystyle f''(-1)= -2\), therefore, it has a relative maximum at x=-1

 

[K_Swiss]

Thanks for the help