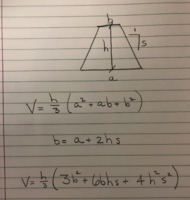Find height of square truncated pyramid based on Volume

[DGBReno]

I have hit a brick wall on this.

I am working with the equation for the volume of a truncated pyramid which is: V = h/3*(a^2+a*b+b^2)
where:
h=height
a=base width
b=top width
V=volume

I am trying to back calculate the height of the pyramid where the knowns are h, b, s, and V.
where:
s=the slope of the side of the pyramid, 1/s rise over run.

I defined the base width (a) in terms of the top width (b) and substituted the result into the starting equation. I end up with a new equation which is still consistent.

My difficulty now is how to rearrange this equation and solve it for h.

Any clues or help would be greatly appreciated.

 

[Dr.Peterson]

At first, I thought you wanted to find the height of the (untruncated) pyramid, given h, b, s, and V. What you are saying is that you want to find h, the height of the frustum, given only b, s, and V. Right?

The trouble is, the equation you got is a cubic equation in h, and it's not easy to do that in a formula. (Try searching for "algebraic solution of cubic" or "cubic formula".) You may end up having to use something like a graphing calculator to solve numerically.

One of the things they forget to teach is that algebra can't solve everything. Some things, in fact, are not only hard, but impossible.