find an equation for the line tangent to the curve
- Thread starter sareen
- Start date
sareen said:
Just use the arc length formula.
\(\displaystyle \int_{0}^{\frac{\pi}{2}}\sqrt{\left(\frac{d}{dt}(2sin(t))\right)^{2}+\left(\frac{d}{dt}(2cos(t))\right)^{2}}dt\)
This whittles down to a very easy integral.
Use \(\displaystyle \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}\)
Then, plug in \(\displaystyle t=\frac{\pi}{4}\) to find the slope at that point. You have \(\displaystyle y=2cos(\frac{\pi}{4}), \;\ x=2sin(\frac{\pi}{4})\)Then, use y=mx+b and solve for b.
BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
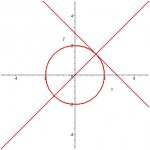
\(\displaystyle Another \ way, \ reverting \ to \ rectangular \ coordinates.\)
\(\displaystyle x \ = \ 2sin(t), \ y \ =2cos(t) \ \implies \ x^{2}+y^{2} \ = \ 4\)
\(\displaystyle a) \ C \ = \ 2\pi r \ = \ 4\pi. \ \frac{C}{4} \ = \ \frac{4\pi}{4} \ = \ \pi.\)
\(\displaystyle b) \ At \ \pi/4 \ m \ =1 \ and \ we \ have \ the \ point \ (\sqrt2,\sqrt2)\)
\(\displaystyle The \ tangent \ line \ is \ perpendicular \ to \ the \ the \ line \ emanating \ from \ the \ origin, \ so \ m \ = \ -1\)
\(\displaystyle with \ point \ (\sqrt2,\sqrt2) \ gives \ equation \ y \ = \ -x+2\sqrt2, \ see \ graph.\)
[attachment=0:37tv7sqs]ghi.jpg[/attachment:37tv7sqs]
\(\displaystyle x \ = \ 2sin(t), \ y \ =2cos(t) \ \implies \ x^{2}+y^{2} \ = \ 4\)
\(\displaystyle a) \ C \ = \ 2\pi r \ = \ 4\pi. \ \frac{C}{4} \ = \ \frac{4\pi}{4} \ = \ \pi.\)
\(\displaystyle b) \ At \ \pi/4 \ m \ =1 \ and \ we \ have \ the \ point \ (\sqrt2,\sqrt2)\)
\(\displaystyle The \ tangent \ line \ is \ perpendicular \ to \ the \ the \ line \ emanating \ from \ the \ origin, \ so \ m \ = \ -1\)
\(\displaystyle with \ point \ (\sqrt2,\sqrt2) \ gives \ equation \ y \ = \ -x+2\sqrt2, \ see \ graph.\)
[attachment=0:37tv7sqs]ghi.jpg[/attachment:37tv7sqs]
