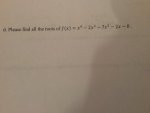Find All The Roots of f (x ) = x^4 - 2x^3 - 7x^2 - 2x - 8.

[CarterS]

(d) Please find all the roots of f (x ) = x ⁴ - 2x ³ - 7x ² - 2x - 8.

---

I know that there should be 4 roots but I can't figure out what they are.

 

[Harry_the_cat]

I know that there should be 4 roots but I can't figure out what they are.

There may or not be 4 REAL roots.

Have you learnt the factor theorem?

From Wikipedia:
The factor theorem states that a polynomial

has a factor

if and only if

(i.e.,

is a root).

 

[CarterS]

Yes

 

[Harry_the_cat]

Yes

Ok. So have you tried f(1), f(-1), f(2), f(-2), f(4), f(-4). If it's going to work "nicely" then you need to try the factors of c (=8 here)

 

[lookagain]

(d) Please find all the roots of f (x ) = x ⁴ - 2x ³ - 7x ² - 2x - 8.

---

I know that there should be 4 roots but I can't figure out what they are.

.

Ok. So have you tried f(1), f(-1), f(2), f(-2), f(4), f(-4). If it's going to work "nicely" then you need to try the factors of c (=8 here)

Don't forget trying f(-8) and f(8), if need be.

CarterS,
also, in \(\displaystyle \ \ f(x) \ = \ x^4 - 2x^3 - 7x^2 - 2x - 8, \ \ \), it would lend itself to factor by grouping if you would rewrite it.
I see a *potential* clue toward using it, because the second and fifth coefficients are the same, and the third
and the last coefficients differ by one.


\(\displaystyle x^4 - 2x^3 - 7x^2 - 2x - 8 \ = \ 0 \)


\(\displaystyle (x^4 - 2x^3 - 8x^2) + (x^2 - 2x - 8) \ = \ 0 \)


\(\displaystyle x^2(x^2 - 2x - 8) + 1(x^2 - 2x - 8) \ = 0 \)


\(\displaystyle (x^2 - 2x - 8)(x^2 + 1) \ = 0 \)


\(\displaystyle (x - 4)(x + 2)(x^2 + 1) \ = 0 \)


What do you do next?