mshireling
New member
- Joined
- Nov 24, 2009
- Messages
- 2
Find the absolute maximum and minimum values of the following functions on the given intervals. Calculators are allowed for arithmetic only. Show all work.
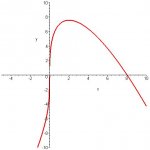
f(x)=x[sup:1ohusltw]1/3[/sup:1ohusltw](8-x) Domain[-1,8]
I need help taking the derivative of this function please!
f(x)=x[sup:1ohusltw]1/3[/sup:1ohusltw](8-x) Domain[-1,8]
I need help taking the derivative of this function please!