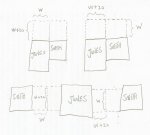
Mr. Smith and Mr. Jones each built a similar stone fence to enclose his backyard. They only enclosed three sides, each using his own house as the fourth side and had a community fence between the two yards. If the total cost was $5 per linear foot, the yards were 20 feet wider than they were deep, and the total cost was $950, what were the length and width of each yard?
any help would be appreciated.
any help would be appreciated.