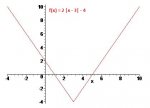
lizzpalmer said:
This is the problem that I am given. And I have figured out that |a| = a if a is greater than or equal to 0 and |a| = -a if a is equal to 0 but beyond that, I have absolutely no idea what this means or how to solve it. They want me to graph it. I'm not looking for the answer because I think that is wrong and doesn't help me learn the concept, but if someone could help explain it in english, that would be great. I'm really struggling in this class and having a hard time grasping the basic concepts. It's an online course, so I don't have anyone to sit down with and explain it to me. Any help would be appreciated. Thank you
Actually, this is a hard problem for a beginner because it involves many concepts at once.
Concept 1. A function is a rule, a map, a machine that goes from one number to the same or another number.
Concept 2. When you graph a function, you are simply drawing a picture of what the function does. As mmm said, the way to do it is to write down some carefully selected input numbers and pair them up with their respective output numbers, and connect the dots with lines or curves. HOWEVER, the absolute value function is a bit unusual because its graph is two different straight lines that intersect.
Concept 3. The absolute value function. I think you understand that rule, but it may help you to graph g(x) = |x| for both positive and negative numbers. Notice that it looks like a V based on a right angle.
Concept 4. Composition of functions. You can combine two or more functions into what can become a very complicated function (called a composite function). Compositions of functions may look complicated, but they just involve using one rule after another (though you have to be careful which order you apply the rules). ALTHOUGH IT IS NEVER NECESSARY AND ADMITTEDLY SLOW, it is frequently helpful to use substitution of variables to understand a composite function. Let's do that with your example.
Let u = x - 3.
Let v = |u|.
Let w = 2v - 4.
So f(x) = w = 2v - 4 = 2|u| - 4 = 2|x - 3| - 4.
OK Let's take an example. Set up a table with column headings of x, u = x - 3, v = |u|, w = 2v - 4
In the next row, pick an initial value for x. Let's try 9. So what is the u that is spit out by the rule u = x - 3 when you give it 9?
Write the answer down in the same row under u.
Now what is the value spit out by the rule v = |u| when you give it the value of u just calculated?
Write that answer down under v in the same row.
Now where does the value of v just written lead you when your map says w = 2v - 4.
Write that answer down under w in the same row.
Did you get 8?
If so, you understand the concept of function, absolute value, and composition of functions.
Now in the next rows try 4, -9, - 4, and 3. What do you get? What does the graph look like?
Does this help?
If you understand inequalities like x - 3 < 0 AND you know how to graph those two lines above over those restricted values of x, this method is also quite easy.