f(x-1) Misunderstanding?

[wlkid9]

Again I'm not sure whether or not I am posting in the correct section, so please excuse me for this.
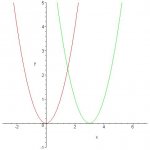
I was looking at the Blue SAT Book and I came across a graph question involving f(x). So they gave me a graph of f(x), then they asked me identify the graph f(x-1). Now first of all, I thought that if x is getting subtracted, shouldn't the graph move to the left since x is getting negative. Apparently, I was wrong and the graph f(x-1) actually moves to the right. From my friends I heard that it is this some weird rule. Can anybody explain this?

Right now, I only really know that f(x) is the same as y. f(x) changes according to the variable x and the end result is y.

 

[mmm4444bot]

f(x - 1): Subtracting 1 from all x shifts the graph one unit to the right.

f(x + 1): Adding 1 to all x shifts the graph one unit to the left.

There's at least two viewpoints for why this happens.

(1) Subtracting 1 from each x on the axis effectively slides the entire coordinate system one unit to the left. If we slide the coordinate system to the left, without moving the graph, then the overall effect is that the graph moves one unit to the right (with respect to the axes).

OR -- a viewpoint that I like:

(2) If we position ourselves on the x-axis at a particular point x, then we're looking at f(x). If we now look to our left one unit, then we see what function f is doing at x - 1. If we want the behavior that's one unit to our left to occur where we are positioned instead, then we need to "pull" the function towards us by one unit. In other words, the graph shifts one unit to the right, where we are, and now it's f(x - 1) instead of f(x).

This concept is a lot easier to explain using visual aids; unfortunately, I can't do that here.

 

[daon]

Re:

OR -- a viewpoint that I like:

(2) If we position ourselves on the x-axis at a particular point x, then we're looking at f(x). If we now look to our left one unit, then we see what function f is doing at x - 1. If we want the behavior that's one unit to our left to occur where we are positioned instead, then we need to "pull" the function towards us by one unit. In other words, the graph shifts one unit to the right, where we are, and now it's f(x - 1) instead of f(x).

I like this one

 

[BigGlenntheHeavy]

[attachment=0:qdojanic]xyz.jpg[/attachment:qdojanic]

My way;

Note: The red graph is f(x) = x^2 and the green graph is g(x) = (x-3)^2.

When x =0, y=0 (for f(x)=x^2) and when x=3, y=0 (for g(x)=(x-3)^2).

If g(x) = (x+3)^2, then x would have to equal -3 for y to equal 0.

Hence, they shift in just the opposite way one would think.

 

[wlkid9]

Ok I was able to punch in the graph on my calc and I did see this weird thing occur but I still don't have like complete understanding of why this happens. Your viewpoint thing didn't really make sense to me.

 

[BigGlenntheHeavy]

Sorry I wasn't able to help you with my "viewpoint thing". Did you look at mmm444bot's two viewpoints? Perhaps someone else, out there in cyber-space, may be able to elucidate on this matter further for your edification. Or, perhaps the problem lies with you or/and your friends who seem to classify anything they can't comprehend as "weird".

 

[daon]

My try:

\(\displaystyle f(x) = \sqrt{x+1}\)
\(\displaystyle g(x) = \sqrt{x}\)

See that \(\displaystyle g(x)=f(x-1)\)?

x-1 lies to the left of x, right? So when we plot \(\displaystyle g(x)\) we are plotting what happened to f one unit "before" our x value.

Using the above functions:
\(\displaystyle f(3)=2\)
\(\displaystyle g(4)=2\)

When graphing g(4) ("f(4-1)"), g asks f what it did when (s)he was at 3. Then g, at x=4, mimics f, when x was 3. Thus it seems f is moving to the right. (In actuality its an entirely different function.)

The same exact argument works for g(x)=f(x+1). Why? Because then f(x)=g(x-1) and this time f is asking the questions. Or, you may switch in the argument any mentionings of "before" with "after", "back" with "ahead", "right" with "left" and minuses with pluses.