Ok I have two homework problems that I'm almost positive are dealing with extreme values. I've usually done those pretty easily with graph functions, but these are word problems...They're really confusing me and I'm not even sure how to start. Help?
1: A closed rectangular container with a square base is to have a volume of 2250 inches cubed. The material for the top and bottom of the container will cost $2 per inch squared and the material for the sides will cost $3 per inch squared. Find the dimensions of the container of the least cost.
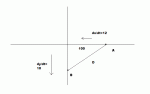
2: At noon ship A was 100 miles due east of ship B. Ship A is sailing west at 12 miles per hour and ship B is sailing south at 10 miles per hour. At what time will the ships be nearest to each other, and what will this distance be?
Thanks!
1: A closed rectangular container with a square base is to have a volume of 2250 inches cubed. The material for the top and bottom of the container will cost $2 per inch squared and the material for the sides will cost $3 per inch squared. Find the dimensions of the container of the least cost.
2: At noon ship A was 100 miles due east of ship B. Ship A is sailing west at 12 miles per hour and ship B is sailing south at 10 miles per hour. At what time will the ships be nearest to each other, and what will this distance be?
Thanks!