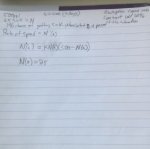I'm in an algebra through modeling class and this is one of the last models we have to complete. I've been struggling with it for a few days, unable to come up with a method or solution for determining the spread of disease. The problem is listed below. I've attached pictures of the work I've come up with (excuse the messy handwriting, I can provide clarification if needed). Thank you!
There are 500 people in the community. Each month, each person will come into contact with
10% of the population, and there’s a 1% chance of transmission of the disease when people
contact each other. At the beginning of the epidemic, there are 25 people who are sick.
Create a method to calculate how many new people get sick each month, and how many total
people are sick each month. Find out what happens to the epidemic after 24 months or so.
First, your one image is rotated 90\(\displaystyle ^\circ\) and I can't read it. The other image is almost as bad as it seems out of focus.
The question revolves around how many [independent] visits there are and the rate of infection. The way you have wrote it, this is a straight linear problem not an exponential one since the infection rate does not depend on the number who are sick. So let's re-write to see if it is more like build a model for the following
-500 population with 25 sick initially
-Each person visits 50 people each month.
-If a non-sick person visits a sick person, there is a 1% chance that the non-sick person will get sick.
Do a simple example
-10 population with 1 sick initially
-Each person visits 2 people [20%] each month.
-If a non-sick person visits a sick person, there is a 1% chance that the non-sick person will get sick.
Now a non-sick person visits 2 people where at each visit they have 10% chance of visiting a sick person. Thus there is a 19% [why?] chance of visiting a sick person or 1.9 sick people were visited by that non-sick person. Having 8 non-sick people means we have 15.2 visits between a sick and non-sick person so that an additional 1% of those get sick, i.e.
-10 population with 2.152 sick at the beginning of the second month
-Each person visits 2 people [20%] each month.
-If a non-sick person visits a sick person, there is a 1% chance that the non-sick person will get sick.
Now a non-sick person visits 2 people where at each visit they have ?% chance of visiting a sick person. Thus there is a ?% chance of visiting a sick person or ? sick people were visited by that non-sick person. Having ? non-sick people means we have ? visits between a sick and non-sick person so that an additional 1% of those get sick,
...
Given the number of sick people at the beginning of the month, what is the formula for the number sick at the beginning of the next month? If you multiply those together, what is the overall formula.
NOTE: It is really better if you can recognize these kind of problems and set up the basic formula almost immediately.