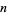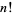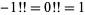I received this problem in class and I am having trouble.
It states:
Define the exponential factorial n!! for positive integers n by 1!!=1 and for n greater than or equal to 1, (n+1)!!= (n+1)^(n!!).
a) Determine the ones digit of 10!!. Explain.
b) Determine the ones digit of 9!!. Explain.
c) Determine the ones digit of 8!!. Explain.
d) Determine, with proof, all digits 0-9 which appear as the ones digit of n!! for at least one positive integer n.
So far I have:
a) 10!!= 3,840 Ones= 0
b) 9!!= 945 Ones=5
c) 8!!= 384 Ones= 4
d) I know that this must be proven by induction. I know that the base case is when n=0. However, I do not know how to continue with the proof.
Thank you for the help in advance.
It states:
Define the exponential factorial n!! for positive integers n by 1!!=1 and for n greater than or equal to 1, (n+1)!!= (n+1)^(n!!).
a) Determine the ones digit of 10!!. Explain.
b) Determine the ones digit of 9!!. Explain.
c) Determine the ones digit of 8!!. Explain.
d) Determine, with proof, all digits 0-9 which appear as the ones digit of n!! for at least one positive integer n.
So far I have:
a) 10!!= 3,840 Ones= 0
b) 9!!= 945 Ones=5
c) 8!!= 384 Ones= 4
d) I know that this must be proven by induction. I know that the base case is when n=0. However, I do not know how to continue with the proof.
Thank you for the help in advance.