Existence of Point where Two Tangent Lines are Parallel

[turophile]

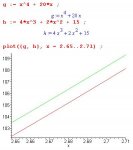
Here's the problem:

Show that there is a number x in the interval (1, 3) at which the tangents to the graphs of y = x[sup:2o6qr407]4[/sup:2o6qr407] + 20x and y = 4x[sup:2o6qr407]3[/sup:2o6qr407] + 2x[sup:2o6qr407]2[/sup:2o6qr407] + 15 are parallel.

Here's what I did:

Since g'(x) and h'(x) are the slopes of the lines tangent to g and h at x, the tangents are parallel when g'(x) = h'(x) or when g'(x) – h'(x) = 0. Let f(x) = g(x) – h(x) = x[sup:2o6qr407]4[/sup:2o6qr407]4 – 4x[sup:2o6qr407]3[/sup:2o6qr407] – 2x[sup:2o6qr407]2[/sup:2o6qr407] + 20x + 15. Then f'(x) = g'(x) – h'(x) = 4x[sup:2o6qr407]3[/sup:2o6qr407] – 12x[sup:2o6qr407]2[/sup:2o6qr407] – 4x + 20 = 0. By the MVT, there is a point z between 1 and 3 for which f'(3) – f'(1) = (3 – 1)0 = 0. This is what needed to be shown.

My questions:

Is my logic correct on this? Is that all there is to solving this type of problem? Or do I need to come up with the x where the tangents are parallel? Looking at the graph of f'(x), there is a value of x where f'(x) = 0 such that 1 < x < 3, but the question wording doesn't seem to require that I solve for it.

 

[mmm4444bot]

the question wording doesn't seem to require that I solve for [x]

I agree. The exercise does not ask for either of the actual two values of x where g`(x) = h`(x).

Regarding your conclusion from the MVT, I think your logic is wrong.

(It looks like your post contains some typographical errors, too. I was confused.)

Let's define g and h. It's good form to always define function names at the beginning with explicit statements.

g(x) = x^4 + 20x

h(x) = 4x^3 + 2x^2 + 15

I'm thinking that it's not necessary to define f(x) = g(x) - h(x). I'm going to use the name f for something else below.

Now, your logic that g`(x) = h`(x) at any x where the slope of functions g and h are equal is very good.

Your result that g`(x) - h`(x) = 4x^3 - 12x^2 - 4x + 20 is also good.

Since we're interested in g`(x) - h`(x) = 0, I'll make the following definition.

f(x) = 4x^3 - 12x^2 - 4x + 20

So, this exercise requires showing that function f has at least one zero such that 1 < x < 3.

Here's where I think you went astray with the MVT.

It appears that you calculated [f(3) - f(1)]/(3 - 1) = 0

This result only tells us that the slope of f is zero somewhere between x = 1 and x = 3 (i.e., there is a local extreme within this interval). The MVT does not tell us whether or not f has a zero there.

In other words, we're talking about f(x) = 0, not f`(x) = 0.

Let us know if you don't understand the difference.

Think about how you could deduce that the curve of f must cross the x-axis at least once between x = 1 and x = 3. Hint: Intermediate Value Theorem using the values of f(x) at x = 1, x = 3, and where f`(x) = 0.

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ x^4+20x \ \ on \ interval \ (1,3) \ and \ g(x) \ = \ 4x^3+2x^2+15\)

\(\displaystyle f'(c) \ = \ \frac{f(b)-f(a)}{b-a} \ and \ g'(c) \ = \ \frac{g(b)-g(a)}{b-a}\)

\(\displaystyle f'(c) \ = \ \frac{141-21}{3-1} \ = \ 60 \ and \ g'(c) \ = \ \frac{141-21}{3-1} \ = \ 60 \ = \ m\)

\(\displaystyle Hence, \ f(1) \ = \ 21 \ and \ m \ = \ 60 \ gives \ y \ = \ 60x-34\)

\(\displaystyle Also, \ 4x^3+20 \ = \ 60, \ x \ = \ 2.154\)

\(\displaystyle f(2.154) \ = \ 64.633, \ hence \ y \ = \ 60x-64.607\)

\(\displaystyle Finally, \ 12x^2+4x \ = \ 60, \ x \ = \ 2.076\)

\(\displaystyle g(2.076) \ = \ 59.408 \ gives \ y \ = \ 60x-65.152\)

\(\displaystyle See \ graph.\)

[attachment=0:3t2pl58u]kkk.jpg[/attachment:3t2pl58u]

 

[mmm4444bot]

Following the lead of the original poster (using names g and h, as implied), but using the definition for f as in my first response, there are two values of x within the interval [1, 3] where the tangents of functions g and h are parallel.

(I'm rounding to four places.)

It's relatively easy to find that f`(2.1547) = 0

f(2.1547) = -4.3168

This shows that local extreme lies below the x-axis.

At the endpoints of interval [1, 3], function f is eight units above the x-axis.

f(1) = 8

f(3) = 8

The IVT tells us that function f takes on every value from 8 counting down to -4.3168 (at the local maximum) before turning around and taking on every value from -4.3168 counting up to 8, as x goes from 1 to 3.

Well, that means that f(x) is zero at two places, in this interval.

So, there are two places within [1, 3] where the tangents to g and h are parallel.

The actual two values are not required, for this exercise, but I find them to be x = 1.5392 or x = 2.6751.

MVR5 plots both functions g (green) and h (hot red) below over a tiny subinterval around these two locations. Encouragingly, the curves appear to have parallel tangents.

(Double-click images, to expand.)

[attachment=1:3o401mrs]first.JPG[/attachment:3o401mrs]

[attachment=0:3o401mrs]second.JPG[/attachment:3o401mrs]

 

[soroban]

Hello, turophile!

There are two solutions.

\(\displaystyle \text{Show that there is a number }x\text{ in the interval }(1, 3)\text{ at which the tangents}\)

. . \(\displaystyle \text{to the graphs of: }\:y \:=\: x^4 + 20x\:\text{ and }\:y \:=\: 4x^3 + 2x^2 + 15\:\text{ are parallel.}\)

If the tangents are parallel, the two derivatives are equal:

. . \(\displaystyle 4x^3 +\;20 \;\;=\;\;12x^2 +\;4x \qquad\Rightarrow\qquad 4x^3 -\;12x^2 -\;4x\;+\;20 \;\;=\;\;0 \qquad\Rightarrow\qquad x^3 \;-\; 3x^2 \;-\; x \;+\; 5 \;\;=\:\;0\)


\(\displaystyle \text{The question becomes:}\)
. . \(\displaystyle \text{Does the cubic }f(x) \:=\:x^3-\;3x^2-\;x\;+\;5\:\text{ have an }x\text{-intercept on the interval }(1,3)\;?\)


\(\displaystyle \text{We find that: }\;\begin{array}{ccc}f(1) &=& +2 \\ f(2) &=& -1 \\ f(3) &=& +2 \end{array}\)


\(\displaystyle \text{Since the cubic is continuous, it has an }x\text{-intercept on the interval }(1,2)\,and\text{ on the interval }(2,3).\)

 

[mmm4444bot]

Ah, Soroban employed the 'ol 1-2-3 strategy. Good for him; less "rigor" saves time.