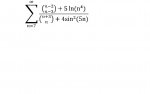Examine the convergence of the series

[problem1]

Hello

Here is another problem: examine the convergence of the series: ? (from n=7 to ?) ( ((n-2)¦(n-3))+5 ln (n^4) ) / ( ((n+3)¦(n))+4sin^2 (5n) )

Anyone that can solve this?

If there is any problem with the equation then look at the picture i attached to this message.

 

[pka]

\(\displaystyle A=\left( {\begin{array}{*{20}c} {n - 2} \\ {n - 3} \\\end{array}} \right) = n - 2\quad ,\quad B=\left( {\begin{array}{*{20}c} {n + 3} \\ n \\\end{array}} \right) = \frac{{\left( {n + 3} \right)\left( {n + 2} \right)\left( {n + 1} \right)}}{6}\)
\(\displaystyle \frac{{A + 5\ln \left( {n^4 } \right)}}{{B + 4\sin ^2 (5n)}} \le \frac{{A + 20n}}{B}\)

If you understand the basic comparision test, then you will see convergence at once.

 

[problem1]

If I will be honest, its been while since i study this, and i remembered that it was quite difficulty.

 

[pka]

If I will be honest, its been while since i study this, and i remembered that it was quite difficulty.

Well using the above \(\displaystyle \frac{{A + 20n}}{B} = \frac{{126n - 12}}{{\left( {n + 3} \right)\left( {n + 2} \right)\left( {n + 1} \right)}}\).

Now \(\displaystyle \sum\limits_{n = 7}^\infty {\frac{{126n - 12}}{{\left( {n + 3} \right)\left( {n + 2} \right)\left( {n + 1} \right)}}}\) converges when comparied with \(\displaystyle \sum\limits_{n = 7}^\infty {\frac{1}{{n^2 }}}\).

Thus the series converges.

 

[problem1]

Ahh, okej, so with the compair method i will get converges (is it ? an / bn)? and then alpha, in 1/n^2 is converges if it is >1, or?