The question is as follows: Evaluate the line integral
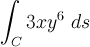 where C is the right half of the circle
where C is the right half of the circle
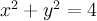
I'm getting (3*4*4^6*4*(2/7), or 56173.7142857143, using the parameterization
x=4cos(t)
y=4sin(t)
Here's the best I could do at typing out my work, sorry if it's difficult to follow, I'm new at typing this stuff out:
My understanding of how a line integral works is that you Parameterize x and y with respect to t, which I've done. Then you do a substitution of the parameterizations into the function to be integrated, and you multiply this whole integral by the arclength, equal to the square root of the derivative of the x parameterization with respect to t squared added to the derivative of the y parameterization with respect to t squared.
So dx/dt should be -4sin(t) and dy/dt should be 4cos(t), so the arclength function should come out to sqrt((-4sin(t))^2+(4cos(t))^2) which should come out to sqrt(16sin^2(t)+16cos^2(t)), so sqrt(16(sin^2(t)+cos^2(t)) so sqrt(16), so 4.
C should be -pi/2 less than or equal to 't' less than or equal to pi/2, making those the limits of integration for the function.
So the integral seems like it should be as follows: Integrate from -pi/2 to pi/2: 3(4cos(t))(4sin(t))^6 times 4 for arclength dt
Which equals: 3*4 times the integral from -pi/2 to pi/2 of:4cos(t)4^6sin^6(t) dt.
Which equals 3*4*4^6*4 times the integral from -pi/2 to pi/2 of: cos(t)sin^6(t) dt
Which equals 3*4*4^6*4*sin^7(t)/7 evaluated from -pi/2 to pi/2
Which equals 3*4*4^6*4/7*(sin^7(pi/2)-sin^7(-pi/2))
Which equals 3*4*4^6*4/7*(1-(-1))
Which equals 3*4*4^6*4*2/7
Our little online homework submittal utility insists that this is incorrect, but I've done this a few times and can't seem to figure out where I'm going wrong. Let me know if you need clarification or anything too, I'm sure I could have messed it up somewhere along the line.
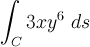
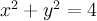
I'm getting (3*4*4^6*4*(2/7), or 56173.7142857143, using the parameterization
x=4cos(t)
y=4sin(t)
Here's the best I could do at typing out my work, sorry if it's difficult to follow, I'm new at typing this stuff out:
My understanding of how a line integral works is that you Parameterize x and y with respect to t, which I've done. Then you do a substitution of the parameterizations into the function to be integrated, and you multiply this whole integral by the arclength, equal to the square root of the derivative of the x parameterization with respect to t squared added to the derivative of the y parameterization with respect to t squared.
So dx/dt should be -4sin(t) and dy/dt should be 4cos(t), so the arclength function should come out to sqrt((-4sin(t))^2+(4cos(t))^2) which should come out to sqrt(16sin^2(t)+16cos^2(t)), so sqrt(16(sin^2(t)+cos^2(t)) so sqrt(16), so 4.
C should be -pi/2 less than or equal to 't' less than or equal to pi/2, making those the limits of integration for the function.
So the integral seems like it should be as follows: Integrate from -pi/2 to pi/2: 3(4cos(t))(4sin(t))^6 times 4 for arclength dt
Which equals: 3*4 times the integral from -pi/2 to pi/2 of:4cos(t)4^6sin^6(t) dt.
Which equals 3*4*4^6*4 times the integral from -pi/2 to pi/2 of: cos(t)sin^6(t) dt
Which equals 3*4*4^6*4*sin^7(t)/7 evaluated from -pi/2 to pi/2
Which equals 3*4*4^6*4/7*(sin^7(pi/2)-sin^7(-pi/2))
Which equals 3*4*4^6*4/7*(1-(-1))
Which equals 3*4*4^6*4*2/7
Our little online homework submittal utility insists that this is incorrect, but I've done this a few times and can't seem to figure out where I'm going wrong. Let me know if you need clarification or anything too, I'm sure I could have messed it up somewhere along the line.
