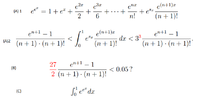We are examining how to estimate integrals we can't estimae using the usual rules (Taylor's formula).
Use the fact that 2 < e < 3 and that g(x) = e^x is increasing. (You do not have to explain this, it is given in the exercise)
A)
1. Explain that for all real numbers x and all natural numbers n
e^(e^x) = 1+ e^x + (e^(2x))/2 + (e^(3x))/5 + ... + e^(Sx) *((e^((n+1)x) )/(n+1)! for an S in (0, e^x)
2. Explain that
( e^(n+1) - 1 )/(n+1)(n+1)! < \integral_0^1{ (e^(Sx) * \frac{ e^((n+1)x){(n+1)!} < (3^3) * \frac{ e^(n+1) - 1 }{ (n+1)(n+1)! }
B)
Find n such that 27/2 * \frac{ e^(n+1) - 1 }{ (n+1)(n+1)! } < 0.05
C)
Use the information gained from (A) and (B) to calculate the integral_0^1 e^(e^x) dx with an error less than 0.05.
Use the fact that 2 < e < 3 and that g(x) = e^x is increasing. (You do not have to explain this, it is given in the exercise)
A)
1. Explain that for all real numbers x and all natural numbers n
e^(e^x) = 1+ e^x + (e^(2x))/2 + (e^(3x))/5 + ... + e^(Sx) *((e^((n+1)x) )/(n+1)! for an S in (0, e^x)
2. Explain that
( e^(n+1) - 1 )/(n+1)(n+1)! < \integral_0^1{ (e^(Sx) * \frac{ e^((n+1)x){(n+1)!} < (3^3) * \frac{ e^(n+1) - 1 }{ (n+1)(n+1)! }
B)
Find n such that 27/2 * \frac{ e^(n+1) - 1 }{ (n+1)(n+1)! } < 0.05
C)
Use the information gained from (A) and (B) to calculate the integral_0^1 e^(e^x) dx with an error less than 0.05.