amathproblemthatneedsolve
Junior Member
- Joined
- May 12, 2019
- Messages
- 189
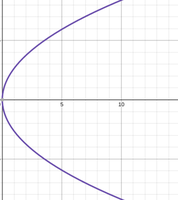
I want to know what the equation is to set the distance between the upper and lower curves of a parabola. e,g finding where the height is 1m. between the upper and lower curve.
The equation is in the form [MATH]y^2=4ax [/MATH]Hopefully this makes sense.
The equation is in the form [MATH]y^2=4ax [/MATH]Hopefully this makes sense.
Last edited: