Epsilon Delta Help

[mop969]

My Calculus teacher tried to explain to me how to solve this problem but it was no help. Can you pleases explain the steps to solve this problem. Thanks.

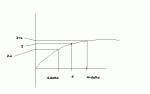
Use the given graph of f(x) = ?x to find a number ? that fulfills the following condition.
if absolute value(x-4) < delta then absolute value(sqrt(x)) - 2) < 0.4
? =


Thanks Again for the help.

 

[galactus]

In this problem, you have an epsilon of \(\displaystyle {\epsilon}=.4\)

I have a diagram to help picture what is going on, though it is not to scale.

Your problem is \(\displaystyle \lim_{x\to 4}\sqrt{x}=2\)

So, find \(\displaystyle |x-4|<{\delta} \;\ s.t. \;\ |\sqrt{x}-2|<{\epsilon}\)

Look at the graph. Can you find delta from that?. Note that \(\displaystyle \epsilon=.4\). So, on the y axis we have 2+.4=2.4 and 2-.4=1.6

 

[daon]

I'm TAing for a class that uses this book :mrgreen:

 

[mop969]

I understand what you did but on the graph 4+delta and 4-delta has me lost. How do you find the delta Thanks.

 

[BigGlenntheHeavy]

\(\displaystyle \lim_{x\to4} \sqrt x \ = \ 2\)

\(\displaystyle Then, \ |\sqrt x-2| \ < \ \epsilon, \ \epsilon \ > \ 0 \ whenever \ 0 \ < \ |x-4| \ < \ \delta\)

\(\displaystyle Given: \ \epsilon \ = \ .4, \ find \ \delta.\)

\(\displaystyle So, \ |\sqrt x-2| \ = \ \bigg|\frac{\sqrt x-2}{1}*\frac{\sqrt x+2}{\sqrt x+2}\bigg| \ = \ \bigg|\frac{x-4}{\sqrt x+2}\bigg| \ = \ \frac{|x-4|}{\sqrt x+2}\)

\(\displaystyle Now, \ if \ we \ restrict \ \delta \ so \ that \ \delta \ less \ than \ \ or \ equal \ to \ 4, \ then:\)

\(\displaystyle |x-4| \ < \ 4\)
\(\displaystyle 0 \ < \ x \ < \ 8\)
\(\displaystyle 0 \ < \ \sqrt x \ < \ \sqrt 8\)
\(\displaystyle 2 \ < \ \sqrt x+2 \ < \ \sqrt 8+2\)
\(\displaystyle \frac{1}{2} \ > \ \frac{1}{\sqrt x+2} \ > \ \frac{1}{\sqrt 8+2}\)
\(\displaystyle \frac{1}{\sqrt x+2} \ < \ \frac{1}{2}, \ hence\)

\(\displaystyle \frac{|x-4|}{\sqrt x+2} \ < \ \frac{|x-4|}{2}\)

\(\displaystyle Ergo, \ since \ \ |\sqrt x-2| \ < \ .4, \ then \ if \ we \ let \ \frac{|x-4|}{2} \ < \ .4 \ \implies \ |x-4| \ < \ .8\)

\(\displaystyle So \ \delta \ = \ .8 \ QED\)

 

[mop969]

I follow you until you put everything over 1 why did you do that? Thanks

 

[BigGlenntheHeavy]

\(\displaystyle Because \ |\sqrt x-2| \ = \ \frac{|x-4|}{\sqrt x+2} \ < \ .4.\)

\(\displaystyle \frac{|x-4|}{\sqrt x+2} \ < \ \frac{|x-4|}{2}. \ Now \ let \ \frac{|x-4|}{2} \ < \ .4, \ then \ \delta \ = \ .8.\)

\(\displaystyle So \ we \ have \ to \ get \ \sqrt x+2 \ into \ the \ denominator.\)

 

[mop969]

I'm sorry I meant when you put everything in the inequality
where 1/2> etc.

 

[BigGlenntheHeavy]

When you take the multiplicative inverse (reciprocal, for those of you from Rio Linda) of an inequality, you have to change the sense of the inequality.

\(\displaystyle For \ example: \ 3 \ < \ 7, \ however \ \frac{1}{3} \ > \ \frac{1}{7}\)