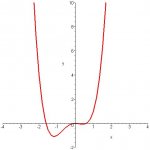
I am facing a problem with the following question:
"For the function f(x)=(x^(1/3))((x^3)+(x^2)-x), find the critical values and local extrema, describe the intervals in which the function is in/de-creasing, and sketch the graph of f(x)".
Now, I know how to answer the question: find the derivative, find critical values (where f'(x)=0), analyse f'(x) for x-values around the CV's to determine minima/maxima, describe the intervals where f(x) is in/de-creasing accordingly, plug CV's into f(x) to get y-values, find roots of f(x), sketch y=f(x).
But, when checking the shape of the graph with online plotters/graphing software, they only show the function for positive x-values. Why is the function undefined for negative x-values? We do not need to worry about a negative denominator, or a negative x-value in a positive root. There is a cube root in the definition of f(x), but we can put any x-values into it, including negative values. So, why can f(x) not take negative x-values?
Kind regards.
"For the function f(x)=(x^(1/3))((x^3)+(x^2)-x), find the critical values and local extrema, describe the intervals in which the function is in/de-creasing, and sketch the graph of f(x)".
Now, I know how to answer the question: find the derivative, find critical values (where f'(x)=0), analyse f'(x) for x-values around the CV's to determine minima/maxima, describe the intervals where f(x) is in/de-creasing accordingly, plug CV's into f(x) to get y-values, find roots of f(x), sketch y=f(x).
But, when checking the shape of the graph with online plotters/graphing software, they only show the function for positive x-values. Why is the function undefined for negative x-values? We do not need to worry about a negative denominator, or a negative x-value in a positive root. There is a cube root in the definition of f(x), but we can put any x-values into it, including negative values. So, why can f(x) not take negative x-values?
Kind regards.