You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Does [1 - x] equal to -1 and why?
- Thread starter 38175425
- Start date
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,307
What is [x]? Are you trying to write the "least integer function," [imath]\lfloor x \rfloor[/imath]?
-Dan
it means Gaussian functionWhat is [x]? Are you trying to write the "least integer function," [imath]\lfloor x \rfloor[/imath]?
-Dan
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,976
Your reply is not at all Helpful! There are many Gaussian functions.it means Gaussian function
Show us your work along with the actual complete question.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,620
As pka said, you'll need to define what you mean by that. It seems likely, from the nature of the problem, that you mean what is shown here, which is the greatest integer, or floor, function.it means Gaussian function
If so, then can you rewrite the entire function for x slightly greater than 1, and for x slightly less than 1?
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,620
I should add that the limit is not 1 by this interpretation; is there a typo? It wouldn't take a big change.As pka said, you'll need to define what you mean by that. It seems likely, from the nature of the problem, that you mean what is shown here, which is the greatest integer, or floor, function.
If so, then can you rewrite the entire function for x slightly greater than 1, and for x slightly less than 1?
Yes. (sorry for replying late)Let me be sure that I am understanding you.
1) The left hand limit = 2
2) The right hand limit = 2
3) Conclude that the limit is 1
Is that what you are saying??
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,620
If the left-hand and right-hand limits are both 2, why would the limit be 1??Sorry for not being clear enough.
My work:
View attachment 34553
Actual complete question:
View attachment 34554
translation:
右極限 = right-hand limit
左極限 = left-hand limit
想像 = imagine
故 = therefore
And what parts of this do you not understand? Your question implied you don't understand any of it. Do you see how my hint explains what they did?
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,561
Let me be sure that I am understanding you.
1) The left hand limit = 2
2) The right hand limit = 2
3) Conclude that the limit is 1
Is that what you are saying??
You seriously need to learn how to tell limits from a graph. If you knew this, then you would never sayYes.
1) The left hand limit = 2
2) The right hand limit = 2
3) Conclude that the limit is 1
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,620
We would be more sure that you understand if you told us in what sense the problem is solved. Do you understand that the final answer given there is incorrect, though the work is correct? Do you understand how each part of the limit works -- namely, that for x between 0 and 1, the expression simplifies to 2+0+0=2, and for x between 1 and 2 it simplifies to 2+1-1=2, so that the limit on each side is 2?Problem solved thank you guys!
The work you showed doesn't take this into account, and seems to be working backward from the solution you were given.
Ok, I will do that.You seriously need to learn how to tell limits from a graph. If you knew this, then you would never say
1) The left hand limit = 2
2) The right hand limit = 2
3) Conclude that the limit is 1
The question and the final answer I posted are from a textbook. Maybe I'll have to ask my math teacher if the textbook did it wrong. Thanks for your explanation.We would be more sure that you understand if you told us in what sense the problem is solved. Do you understand that the final answer given there is incorrect, though the work is correct? Do you understand how each part of the limit works -- namely, that for x between 0 and 1, the expression simplifies to 2+0+0=2, and for x between 1 and 2 it simplifies to 2+1-1=2, so that the limit on each side is 2?
The work you showed doesn't take this into account, and seems to be working backward from the solution you were given.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,620
Yes, that's what I'm suggesting.I think the answer might be a typo, it should be 2.
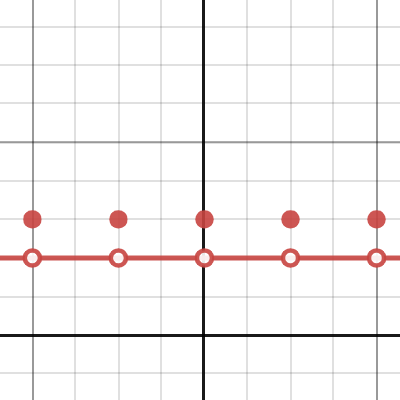
Incidentally, here is a graph of the expression [imath]y=2+\operatorname{floor}\left(x\right)+\operatorname{floor}\left(1-x\right)[/imath] on Desmos:
I think that makes the limit rather clear.
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 544
Beer induced ramblings follow.

 www.desmos.com
www.desmos.com
Unfortunately, Desmos has a glitch; it won't show the where the holes should be....
Incidentally, here is a graph of the expression [imath]y=2+\operatorname{floor}\left(x\right)+\operatorname{floor}\left(1-x\right)[/imath] on Desmos:
I think that makes the limit rather clear.






