Do I have Enough Info?

[BradM73]

Hi, I'm not sure if I have enough info to work out 'x'! By having both diagonals plus the height and width I'm thinking it would be enough. Can anybody help me to work this out? Thanks in advance.

 

[Romsek]

Use the right triangle with sides c, B, and (A+x)


[MATH]c^2 = (A+x)^2 + B^2\\ c^2-B^2 = (A+x)^2\\ \sqrt{c^2-B^2}= A+x\\ x = \sqrt{c^2-B^2}-A = \sqrt{(2971)^2-(2064)^2}-2129 \approx 8[/MATH]

 

[BradM73]

Awesome, you made it so easy. I think I was trying to make it too complicated. Thanks heaps

 

[Dr.Peterson]

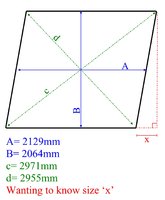
Hi, I'm not sure if I have enough info to work out 'x'! By having both diagonals plus the height and width I'm thinking it would be enough. Can anybody help me to work this out? Thanks in advance.

You actually have too much information. Since you can find x using only A, B, and c, you can find d -- and I don't get exactly the number given! I get 2959.52, not 2955.

 

[BradM73]

You actually have too much information. Since you can find x using only A, B, and c, you can find d -- and I don't get exactly the number given! I get 2959.52, not 2955.

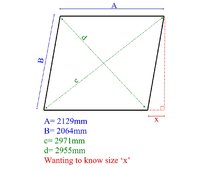
Hi, I thought Romsek solution was correct (and it was for the problem I displayed) until I realised I'd sized it incorrectly. I've attached the correct drawing and I think this makes it a lot harder to solve.

The drawing is of a window opening in a house. I'm ordering internal plantation shutters that have a frame around them that will sit inside the opening. If I order the shutters using the existing width and height (A & B) the frame won't fit as the frame has four 90 degree corners that can't be changed. I'm trying to work out how much I need to deduct from the opening with and height (x) in order to ensure the frame fits in. The two diagonal measurements are real world measurements meaning the opening isn't a perfect rectangle as you alluded to above (I think the correct name for this would be 'Irregular convex quadrilateral', but I might be wrong).

 

[Dr.Peterson]

Nothing here is a rectangle; but the fact that the numbers are not consistent when we assume it's a parallelogram tells me that I can't make any assumptions. You'll have to measure all four sides and one diagonal (or any other 5 measurements) to be sure we have it right. The sixth measurement is a check on the others.

Here is a picture of what I get, showing that if d is 2955, then c turns out to be 2975.47, not 2971. Maybe that's close enough, or maybe not.



In red are the perpendicular height and your x = 14.26 mm.

I did all this in GeoGebra this time; we can talk about how to calculate it once we're sure of everything.

 

[BradM73]

Hi Dr Peterson, thank you for your work on this. As the sizes given are measured from an actual window opening it's possible the timbers are a little bent making it almost impossible for a 100% accurate answer. I believe the answer of 14.26mm is very close and that is close enough.

I used a spirit level on the window opening and my measurement was about 12mm so I think 14mm would be correct. I'd love to learn how to calculate this if possible.

Cheers
Brad

 

[Dr.Peterson]

For this version of the problem (which is significantly harder than the original because no perpendiculars are known), probably the easiest way is trigonometry. Use the Law of Cosines on a triangle (say the one with sides A, B, and d) to find one angle (say the lower left). Then you can use the sine of that angle to find the height, and the cosine to find A+x.

If you need help with that, let me know.